
【題目】已知橢圓![]() 的離心率
的離心率![]() ,左、右焦點分別為
,左、右焦點分別為![]() 、
、![]() ,拋物線
,拋物線![]() 的焦點
的焦點![]() 恰好是該橢圓的一個頂點.
恰好是該橢圓的一個頂點.
(1)求橢圓![]() 的方程;
的方程;
(2)已知圓![]() 的切線
的切線![]() (直線
(直線![]() 的斜率存在且不為零)與橢圓相交于
的斜率存在且不為零)與橢圓相交于![]() 、
、![]() 兩點,那么以
兩點,那么以![]() 為直徑的圓是否經(jīng)過定點?如果是,求出定點的坐標;如果不是,請說明理由.
為直徑的圓是否經(jīng)過定點?如果是,求出定點的坐標;如果不是,請說明理由.
【答案】(1)![]() ;(2)以
;(2)以![]() 為直徑的圓過定點
為直徑的圓過定點![]() .
.
【解析】
(1)根據(jù)拋物線的焦點與橢圓的頂點公式求解即可.
(2) 設(shè)直線![]() 的方程為
的方程為![]() ,聯(lián)立直線與橢圓的方程,列出韋達定理,并根據(jù)直線
,聯(lián)立直線與橢圓的方程,列出韋達定理,并根據(jù)直線![]() 與圓
與圓![]() 相切得出
相切得出![]() 的關(guān)系式,代入證明
的關(guān)系式,代入證明![]() 即可.
即可.
(1)因為橢圓![]() 的離心率
的離心率![]() ,所以
,所以![]() ,即
,即![]() .
.
因為拋物線![]() 的焦點
的焦點![]() 恰好是該橢圓的一個頂點,
恰好是該橢圓的一個頂點,
所以![]() ,所以
,所以![]() .所以橢圓
.所以橢圓![]() 的方程為
的方程為![]() .
.
(2)因為直線![]() 的斜率存在且不為零.故設(shè)直線
的斜率存在且不為零.故設(shè)直線![]() 的方程為
的方程為![]() .
.
由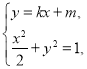 消去
消去![]() ,得
,得![]() ,
,
所以設(shè)![]() ,則
,則![]() .
.
所以![]() .
.
所以![]() .①
.①
因為直線![]() 和圓
和圓![]() 相切,所以圓心到直線
相切,所以圓心到直線![]() 的距離
的距離![]() ,
,
整理,得![]() ,②
,②
將②代入①,得![]() ,顯然以
,顯然以![]() 為直徑的圓經(jīng)過定點
為直徑的圓經(jīng)過定點![]()
綜上可知,以![]() 為直徑的圓過定點
為直徑的圓過定點![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學 來源: 題型:
【題目】如圖,B,C分別是海岸線上的兩個城市,兩城市間由筆直的海濱公路相連,B,C之間的距離為100km,海島A在城市B的正東方50![]() 處.從海島A到城市C,先乘船按北偏西θ角(
處.從海島A到城市C,先乘船按北偏西θ角(![]() ,其中銳角
,其中銳角![]() 的正切值為
的正切值為![]() )航行到海岸公路P處登陸,再換乘汽車到城市C.已知船速為25km/h,車速為75km/h.
)航行到海岸公路P處登陸,再換乘汽車到城市C.已知船速為25km/h,車速為75km/h.
(1)試建立由A經(jīng)P到C所用時間與![]() 的函數(shù)解析式;
的函數(shù)解析式;
(2)試確定登陸點P的位置,使所用時間最少,并說明理由.

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
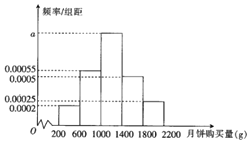
【題目】2018年中秋節(jié)到來之際,某超市為了解中秋節(jié)期間月餅的銷售量,對其所在銷售范圍內(nèi)的1000名消費者在中秋節(jié)期間的月餅購買量![]() 單位:
單位:![]() 進行了問卷調(diào)查,得到如下頻率分布直方圖:
進行了問卷調(diào)查,得到如下頻率分布直方圖:
![]() 求頻率分布直方圖中a的值;
求頻率分布直方圖中a的值;
![]() 以頻率作為概率,試求消費者月餅購買量在
以頻率作為概率,試求消費者月餅購買量在![]() 的概率;
的概率;
![]() 已知該超市所在銷售范圍內(nèi)有20萬人,并且該超市每年的銷售份額約占該市場總量的
已知該超市所在銷售范圍內(nèi)有20萬人,并且該超市每年的銷售份額約占該市場總量的![]() ,請根據(jù)這1000名消費者的人均月餅購買量估計該超市應準備多少噸月餅恰好能滿足市場需求
,請根據(jù)這1000名消費者的人均月餅購買量估計該超市應準備多少噸月餅恰好能滿足市場需求![]() 頻率分布直方圖中同一組的數(shù)據(jù)用該組區(qū)間的中點值作代表
頻率分布直方圖中同一組的數(shù)據(jù)用該組區(qū)間的中點值作代表![]() ?
?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為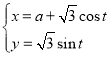 (
(![]() 為參數(shù),
為參數(shù),![]() ),以坐標原點
),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸的極坐標系中,曲線
軸正半軸為極軸的極坐標系中,曲線![]() 上一點
上一點![]() 的極坐標為
的極坐標為![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)設(shè)點![]() 在
在![]() 上,點
上,點![]() 在
在![]() 上(異于極點),若
上(異于極點),若![]() 四點依次在同一條直線
四點依次在同一條直線![]() 上,且
上,且![]() 成等比數(shù)列,求
成等比數(shù)列,求![]() 的極坐標方程.
的極坐標方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系xoy中,以坐標原點O為極點,x軸正半軸為極軸建立極坐標系。已知曲線C的極坐標方程為![]() ,過點
,過點![]() 的直線l的參數(shù)方程為
的直線l的參數(shù)方程為 (為參數(shù)),直線l與曲線C交于M、N兩點。
(為參數(shù)),直線l與曲線C交于M、N兩點。
(1)寫出直線l的普通方程和曲線C的直角坐標方程:
(2)若![]() 成等比數(shù)列,求a的值。
成等比數(shù)列,求a的值。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的極值;
的極值;
(2)若對任意的![]() ,當
,當![]() 時,
時,![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的最大值;
的最大值;
(3)若函數(shù)![]() 恰有兩個不相等的零點,求實數(shù)
恰有兩個不相等的零點,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為了保障全國第四次經(jīng)濟普查順利進行,國家統(tǒng)計局從東部選擇江蘇, 從中部選擇河北. 湖北,從西部選擇寧夏, 從直轄市中選擇重慶作為國家綜合試點地區(qū),然后再逐級確定普查區(qū)域,直到基層的普查小區(qū).在普查過程中首先要進行宣傳培訓,然后確定對象,最后入戶登記. 由于種種情況可能會導致入戶登記不夠順利,這為正式普查提供了寶貴的試點經(jīng)驗. 在某普查小區(qū),共有 50 家企事業(yè)單位,150 家個體經(jīng)營戶,普查情況如下表所示:
普查對象類別 | 順利 | 不順利 | 合計 |
企事業(yè)單位 | 40 | 10 | 50 |
個體經(jīng)營戶 | 100 | 50 | 150 |
合計 | 140 | 60 | 200 |
(1)寫出選擇 5 個國家綜合試點地區(qū)采用的抽樣方法;
(2)根據(jù)列聯(lián)表判斷是否有![]() 的把握認為“此普查小區(qū)的入戶登記是否順利與普查對象的類別有關(guān)”;
的把握認為“此普查小區(qū)的入戶登記是否順利與普查對象的類別有關(guān)”;
(3)以頻率作為概率, 某普查小組從該小區(qū)隨機選擇 1 家企事業(yè)單位,3 家個體經(jīng)營戶作為普查對象,入戶登記順利的對象數(shù)記為![]() , 寫出
, 寫出![]() 的分布列,并求
的分布列,并求![]() 的期望值.
的期望值.
附:![]()
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.88 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系中,曲線![]() 的方程為
的方程為![]() ,以
,以![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 是圓心在極軸上且經(jīng)過極點的圓,射線
是圓心在極軸上且經(jīng)過極點的圓,射線![]() 與曲線
與曲線![]() 交于點
交于點![]() .
.
(1)求曲線![]() 的參數(shù)方程,
的參數(shù)方程,![]() 的極坐標方程;
的極坐標方程;
(2)若![]() ,
,![]() 是曲線
是曲線![]() 上的兩點,求
上的兩點,求![]() 的值.
的值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com