
如圖, 是以
是以 為直徑的半圓上異于點
為直徑的半圓上異于點 的點,矩形
的點,矩形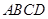 所在的平面垂直于該半圓所在平面,且
所在的平面垂直于該半圓所在平面,且

(Ⅰ)求證: ;
;
(Ⅱ)設(shè)平面 與半圓弧的另一個交點為
與半圓弧的另一個交點為 ,
,
①求證: //
// ;
;
②若 ,求三棱錐E-ADF的體積.
,求三棱錐E-ADF的體積.
(Ⅰ)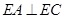 ;(Ⅱ)①
;(Ⅱ)①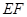 //
//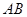 ;②
;②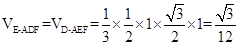 .
.
【解析】
試題分析:(1)證明線線垂直,則可轉(zhuǎn)化為線面垂直,由于圓周角的定義,則知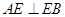 ,由矩形
,由矩形 所在的平面垂直于該半圓所在平面,及面面垂直性質(zhì)定理得
所在的平面垂直于該半圓所在平面,及面面垂直性質(zhì)定理得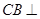 面
面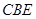 ,則可得平面
,則可得平面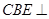 平面
平面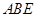
根據(jù)垂直的有關(guān)性質(zhì)定理,則可得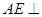 平面
平面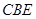 ,故
,故
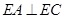
(2)①證明線線平行,則可用過平面的一個平行線作于該平面相交的平面,則該直線與交線平行由 ,得
,得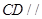 平面
平面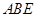 ,又由平面
,又由平面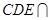 平面
平面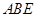 于直線
于直線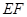 ,則根據(jù)線面平行的性質(zhì)定理得
,則根據(jù)線面平行的性質(zhì)定理得 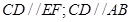 ,由平行的傳遞性得
,由平行的傳遞性得 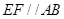 ;②則體積可以用多種方法,有直接求法、割補法、轉(zhuǎn)化法,對于此題可轉(zhuǎn)化后用直接求法,求三棱錐E-ADF先轉(zhuǎn)化
;②則體積可以用多種方法,有直接求法、割補法、轉(zhuǎn)化法,對于此題可轉(zhuǎn)化后用直接求法,求三棱錐E-ADF先轉(zhuǎn)化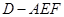 ;根據(jù)三棱錐的體積公式,則有
;根據(jù)三棱錐的體積公式,則有
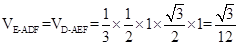
試題解析:
 是半圓上異于
是半圓上異于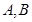 的點,
的點,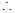
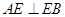 ,又
,又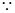 矩形
矩形 所在的平面垂直于該半圓所在平面
所在的平面垂直于該半圓所在平面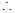 由面面垂直性質(zhì)定理得
由面面垂直性質(zhì)定理得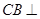 面
面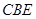 ,
,
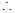 平面
平面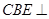 平面
平面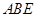
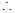
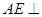 平面
平面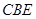 ,故
,故 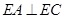 .
.
(2)①
由 ,得
,得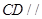 平面
平面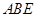 ,又
,又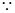 平面
平面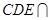 平面
平面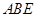 于直線
于直線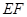 ,
,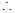 根據(jù)線面平行的性質(zhì)定理得
根據(jù)線面平行的性質(zhì)定理得 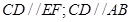 ,故
,故 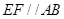 ,②
,②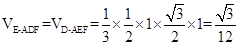 .
.
考點:1.立體幾何的平行垂直的證明,2.立體幾何體積的求解.


科目:高中數(shù)學 來源:2013-2014學年安徽省高三上學期第三次月考文科數(shù)學試卷(解析版) 題型:解答題
如圖, 是以
是以 為直徑的半圓上異于點
為直徑的半圓上異于點 的點,矩形
的點,矩形 所在的平面垂直于該半圓所在平面,且
所在的平面垂直于該半圓所在平面,且

(Ⅰ).求證: ;
;
(Ⅱ).設(shè)平面 與半圓弧的另一個交點為
與半圓弧的另一個交點為 ,
,
①.求證: //
// ;
;
②.若 ,求三棱錐E-ADF的體積.
,求三棱錐E-ADF的體積.
查看答案和解析>>
科目:高中數(shù)學 來源:2014屆福建省高二下學期期中考試文科數(shù)學試卷(解析版) 題型:解答題
如圖, 是以
是以 為直徑的半圓上異于
為直徑的半圓上異于 、
、 的點,矩形
的點,矩形 所在的平面垂直于該半圓所在的平面,且
所在的平面垂直于該半圓所在的平面,且 .
.

(Ⅰ)求證: ;
;
(Ⅱ)設(shè)平面 與半圓弧的另一個交點為
與半圓弧的另一個交點為 .
.
①試證: ;
;
②若 ,求三棱錐
,求三棱錐 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學 來源:2012-2013學年福建省泉州市高三畢業(yè)班質(zhì)量檢查文科數(shù)學試卷(解析版) 題型:解答題
(本小題滿分12分)
如圖, 是以
是以 為直徑的半圓上異于
為直徑的半圓上異于 、
、 的點,矩形
的點,矩形 所在的平面垂直于該半圓所在的平面,且
所在的平面垂直于該半圓所在的平面,且 .
.

(Ⅰ)求證: ;
;
(Ⅱ)設(shè)平面 與半圓弧的另一個交點為
與半圓弧的另一個交點為 .
.
①試證: ;
;
②若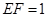 ,求三棱錐
,求三棱錐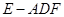 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學 來源:2010-2011學年江蘇省姜堰市高三第一學期學情調(diào)研數(shù)學試卷 題型:解答題
(本試卷共40分,考試時間30分鐘)
21.(選做題)本大題包括A,B,C,D共4小題,請從這4題中選做2小題. 每小題10分,共20分.請在答題卡上準確填涂題目標記. 解答時應(yīng)寫出文字說明、證明過程或演算步驟.
A. 選修4-1:幾何證明選講
如圖, 是邊長為
是邊長為 的正方形,以
的正方形,以 為圓心,
為圓心, 為半徑的圓弧與以
為半徑的圓弧與以 為直徑的半⊙O交于點
為直徑的半⊙O交于點 ,延長
,延長 交
交 于
于 .
.
(1)求證: 是
是 的中點;(2)求線段
的中點;(2)求線段 的長.
的長.

查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com