
【題目】如圖(1),在平面五邊形![]() 中,已知四邊形
中,已知四邊形![]() 為正方形,
為正方形,![]() 為正三角形.沿著
為正三角形.沿著![]() 將四邊形
將四邊形![]() 折起得到四棱錐
折起得到四棱錐![]() ,使得平面
,使得平面![]() 平面
平面![]() ,設
,設![]() 在線段
在線段![]() 上且滿足
上且滿足![]() ,
,![]() 在線段
在線段![]() 上且滿足
上且滿足![]() ,
,![]() 為
為![]() 的重心,如圖(2).
的重心,如圖(2).
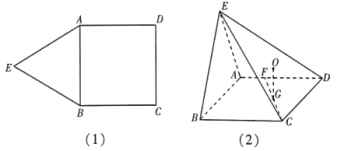
(1)求證:![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)見解析;(2)![]()
【解析】
(1)取![]() 的中點
的中點![]() ,
,![]() 的中點
的中點![]() ,連接
,連接![]() ,可知
,可知![]() 三點共線,
三點共線,![]() 三點共線.,因而可得
三點共線.,因而可得![]() 為
為![]() 的重心,再利用線面平行的判定,及可證出;
的重心,再利用線面平行的判定,及可證出;
(2)根據條件,通過面面垂直的性質,證出![]() 平面
平面![]() ,建立空間直角坐標系,標點,求
,建立空間直角坐標系,標點,求![]() 及平面
及平面![]() 的法向量為
的法向量為![]() ,通過利用空間向量法求出線面角.
,通過利用空間向量法求出線面角.
(1)如圖,取![]() 的中點
的中點![]() ,
,![]() 的中點
的中點![]() ,連接
,連接![]() .
.
由已知易得![]() 三點共線,
三點共線,![]() 三點共線.
三點共線.
因為![]() ,
,![]() ,所以
,所以![]() .
.
又![]() 為
為![]() 的重心,所以
的重心,所以![]() ,
,
所以![]() .
.
因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
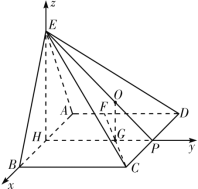
(2)在![]() 中,因為
中,因為![]() 為
為![]() 的中點,所以
的中點,所以![]() .
.
因為平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
由(1)得,![]() .
.
所以![]() 兩兩垂直,如圖,
兩兩垂直,如圖,
分別以射線![]() 的方向為
的方向為![]() 軸的正方向建立空間直角坐標系
軸的正方向建立空間直角坐標系![]() .
.
設![]() ,因為
,因為![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() ,
,![]() .
.
所以![]() ,
, ,
,![]() ,
,![]() .
.
所以 ,
,![]() ,
,![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,則
,則
所以 令
令![]() ,則
,則![]() ,所以可取
,所以可取![]() .
.
設直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,則
,則
 .
.


科目:高中數學 來源: 題型:
【題目】2018年6月14日,世界杯足球賽在俄羅斯拉開帷幕,世界杯給俄羅斯經濟帶來了一定的增長,某紀念商品店的銷售人員為了統計世界杯足球賽期間商品的銷售情況,隨機抽查了該商品商店某天200名顧客的消費金額情況,得到如圖頻率分布表:將消費顧客超過4萬盧布的顧客定義為”足球迷”,消費金額不超過4萬盧布的顧客定義為“非足球迷”。
消費金額/萬盧布 |
|
|
|
|
|
| 合計 |
顧客人數 | 9 | 31 | 36 | 44 | 62 | 18 | 200 |
(1)求這200名顧客消費金額的中位數與平均數(同一組中的消費金額用該組的中點值作代表;
(2)該紀念品商店的銷售人員為了進一步了解這200名顧客喜歡紀念品的類型,采用分層抽樣的方法從“非足球迷”,“足球迷”中選取5人,再從這5人中隨機選取3人進行問卷調查,則選取的3人中“非足球迷”人數的分布列和數學期望。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《算法統宗》是中國古代數學名著,由明代數學家程大位所著,該作完善了珠算口訣,確立了算盤用法,完成了由籌算到珠算的徹底轉變,該作中有題為“李白沽酒”“李白街上走,提壺去買酒。遇店加一倍,見花喝一斗,三遇店和花,喝光壺中酒。借問此壺中,原有多少酒?”,如圖為該問題的程序框圖,若輸出的![]() 值為0,則開始輸入的
值為0,則開始輸入的![]() 值為( )
值為( )
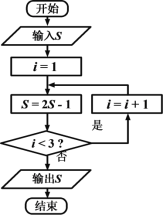
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直四棱柱ABCD–A1B1C1D1中,已知底面ABCD是菱形,點P是側棱C1C的中點.
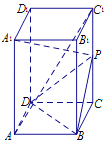
(1)求證:AC1∥平面PBD;
(2)求證:BD⊥A1P.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業要設計制造一批大小、規格相同的長方體封閉水箱,已知每個水箱的表面積為432(每個水箱的進出口所占面積與制作材料的厚度均忽略不計).每個長方體水箱的底面長是寬的2倍.現設每個長方體水箱的底面寬是![]() ,用
,用![]() 表示每個長方體水箱的容積.
表示每個長方體水箱的容積.
(1)試求函數![]() 的解析式及其定義域;
的解析式及其定義域;
(2)當![]() 為何值時,
為何值時,![]() 有最大值,并求出最大值.
有最大值,并求出最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一種拋硬幣游戲的規則是:拋擲一枚硬幣,每次正面向上得1分,反面向上得2分.
(1)設拋擲5次的得分為![]() ,求
,求![]() 的分布列和數學期望
的分布列和數學期望![]() ;
;
(2)求恰好得到![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法錯誤的是( )
A.“![]() ”是“
”是“![]() ”的充分不必要條件
”的充分不必要條件
B.若![]() 為假命題,則
為假命題,則![]() ,
,![]() 均為真命題
均為真命題
C.命題“若![]() ,則
,則![]() ”的逆否命題是“若
”的逆否命題是“若![]() ,則
,則![]() |”
|”
D.若命題![]() ,使得
,使得![]() ,則
,則![]() ,恒有
,恒有![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年非洲豬瘟在東北三省出現,為了進行防控,某地生物醫藥公司派出技術人員對當地甲乙兩個養殖場提供技術服務,方案和收費標準如下:
方案一,公司每天收取養殖場技術服務費40元,對于需要用藥的每頭豬收取藥費2元,不需要用藥的不收費;
方案二,公司每天收取養殖場技術服務費120元,若需要用藥的豬不超過45頭,不另外收費,若需要用藥的豬超過45頭,超過部分每天收取藥費8元.
(1)設日收費為![]() (單位:元),每天需要用藥的豬的數量為
(單位:元),每天需要用藥的豬的數量為![]() ,試寫出兩種方案中
,試寫出兩種方案中![]() 與
與![]() 的函數關系式.
的函數關系式.
(2)若該醫藥公司從10月1日起對甲養殖場提供技術服務,10月31日該養殖場對其中一個豬舍9月份和10月份豬的發病數量進行了統計,得到如下![]() 列聯表.
列聯表.
9月份 | 10月份 | 合計 | |
未發病 | 40 | 85 | 125 |
發病 | 65 | 20 | 85 |
合計 | 105 | 105 | 210 |
根據以上列聯表,判斷是否有![]() 的把握認為豬未發病與醫藥公司提供技術服務有關.
的把握認為豬未發病與醫藥公司提供技術服務有關.
附:![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
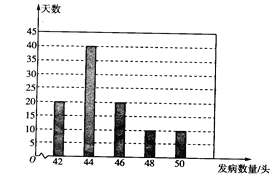
(3)當地的丙養殖場對過去100天豬的發病情況進行了統計,得到如上圖所示的條形統計圖.依據該統計數據,從節約養殖成本的角度去考慮,若丙養殖場計劃結合以往經驗從兩個方案中選擇一個,那么選擇哪個方案更合適,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com