
【題目】記![]() 表示
表示![]() ,
,![]() 中的最大值,如
中的最大值,如![]()
![]() .已知函數
.已知函數![]() ,
,![]() .
.
(1)設![]() ,求函數
,求函數![]() 在
在![]() 上零點的個數;
上零點的個數;
(2)試探討是否存在實數![]() ,使得
,使得![]() 對
對![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
【答案】(1)![]() 個;(2)存在,
個;(2)存在,![]() .
.
【解析】
試題分析:(1)設![]() ,利用導數與單調性的關系求出
,利用導數與單調性的關系求出![]() ,可得
,可得![]() ,則
,則![]() ,結合圖象可得零點的個數;(2)可將題意轉化為
,結合圖象可得零點的個數;(2)可將題意轉化為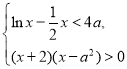 對
對![]() 恒成立,分別求
恒成立,分別求![]() 和
和![]() 成立即可.
成立即可.
試題解析:(1)設![]() ,
,![]() ,
,
令![]() ,得
,得![]() ,
,![]() 遞增;令
遞增;令![]() ,得
,得![]() ,
,![]() 遞減.
遞減.
∴![]() ,∴
,∴![]() ,即
,即![]() ,∴
,∴![]() .
.
設![]() ,結合
,結合![]() 與
與![]() 在
在![]() 上圖象可知,這兩個函數的圖象在
上圖象可知,這兩個函數的圖象在![]() 上有兩個交點,即
上有兩個交點,即![]() 在
在![]() 上零點的個數為
上零點的個數為![]() .
.
(2)假設存在實數![]() ,使得
,使得![]() 對
對![]() 恒成立,
恒成立,
則 對
對![]() 恒成立,
恒成立,
即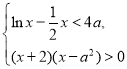 對
對![]() 恒成立,
恒成立,
(i)設![]() ,
,![]()
![]() ,
,
令![]() ,得
,得![]() ,
,![]() 遞增;令
遞增;令![]() ,得
,得![]() ,
,![]() 遞減.
遞減.
∴![]() .
.
當![]() ,即
,即![]() 時,
時,![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
故當![]() 時,
時,![]() 對
對![]() 恒成立.
恒成立.
當![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上遞減,∴
上遞減,∴![]() .
.
∵![]() ,∴
,∴![]()
故當![]() 時,
時,![]() 對
對![]() 恒成立.
恒成立.
(ii)若![]() 對
對![]() 恒成立,則
恒成立,則![]() ,∴
,∴![]() .
.
由(i)及(ii)得,![]() .
.
故存在實數![]() ,使得
,使得![]() 對
對![]() 恒成立,
恒成立,
且![]() 的取值范圍為
的取值范圍為![]() .
.


 星級口算天天練系列答案
星級口算天天練系列答案科目:高中數學 來源: 題型:
【題目】某單位每天的用電量![]() (度)與當天最高氣溫
(度)與當天最高氣溫![]() (℃)之間具有線性相關關系,下表是該單位隨機統計4天的用電量與當天最高氣溫的數據.
(℃)之間具有線性相關關系,下表是該單位隨機統計4天的用電量與當天最高氣溫的數據.
最高氣溫(℃) | 26 | 29 | 31 | 34 |
用電量 (度) | 22 | 26 | 34 | 38 |
(Ⅰ)根據表中數據,求出回歸直線的方程![]() (其中
(其中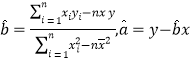 );
);
(Ⅱ)試預測某天最高氣溫為33℃時,該單位當天的用電量(精確到1度).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com