
【題目】已知實(shí)數(shù)a>0, ![]() 方程
方程 ![]() 有且僅有兩個(gè)不等實(shí)根,且較大的實(shí)根大于3,則實(shí)數(shù)a的取值范圍 .
有且僅有兩個(gè)不等實(shí)根,且較大的實(shí)根大于3,則實(shí)數(shù)a的取值范圍 .
【答案】![]()
【解析】解:設(shè)比較大的根為x1 , 則x1>3, 此時(shí)由 ![]() =log3x>log33=1,
=log3x>log33=1,
即a ![]() ,即a
,即a ![]() .
.
∵方程 ![]() 有且僅有兩個(gè)不等實(shí)根,
有且僅有兩個(gè)不等實(shí)根,
∴當(dāng)x≤1時(shí),方程 ![]() 有且僅有1實(shí)根,
有且僅有1實(shí)根,
即﹣x ![]() ,在x≤1時(shí),只有一個(gè)根.
,在x≤1時(shí),只有一個(gè)根.
∴x ![]() ,
,
設(shè)g(x)=x ![]() ,(x≤1),
,(x≤1),
函數(shù)的對(duì)稱(chēng)軸為x=a,
若a≥1,
∵g(0)= ![]() ,
,
∴此時(shí)滿足g(1)≤0,(圖1)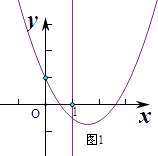
即g(1)=1﹣2a+ ![]() ≤0,
≤0,
∴7a2﹣32a+16≤0,
解得 ![]() ,∴此時(shí)1≤a≤4,.
,∴此時(shí)1≤a≤4,.
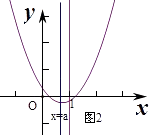
若0<a<1,
∵g(0)= ![]() ,
,
∴此時(shí)滿足g(1)<0,
即g(1)=1﹣2a+ ![]() <0,
<0,
∴77a2﹣32a+16<0,
解得 ![]() ,∴此時(shí)
,∴此時(shí) ![]() ,
,
∴ ![]() ,
,
又a ![]() ,
,
∴ ![]() ,
,
即實(shí)數(shù)a的取值范圍是 ![]() ,
,
所以答案是: ![]() .
.
【考點(diǎn)精析】關(guān)于本題考查的函數(shù)的零點(diǎn)與方程根的關(guān)系和函數(shù)的零點(diǎn),需要了解二次函數(shù)的零點(diǎn):(1)△>0,方程 有兩不等實(shí)根,二次函數(shù)的圖象與 軸有兩個(gè)交點(diǎn),二次函數(shù)有兩個(gè)零點(diǎn);(2)△=0,方程 有兩相等實(shí)根(二重根),二次函數(shù)的圖象與 軸有一個(gè)交點(diǎn),二次函數(shù)有一個(gè)二重零點(diǎn)或二階零點(diǎn);(3)△<0,方程 無(wú)實(shí)根,二次函數(shù)的圖象與 軸無(wú)交點(diǎn),二次函數(shù)無(wú)零點(diǎn);函數(shù)的零點(diǎn)就是方程的實(shí)數(shù)根,亦即函數(shù)的圖象與軸交點(diǎn)的橫坐標(biāo).即:方程有實(shí)數(shù)根,函數(shù)的圖象與坐標(biāo)軸有交點(diǎn),函數(shù)有零點(diǎn)才能得出正確答案.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖是正四面體的平面展開(kāi)圖,G,H,M,N分別為DE,BE,EF,EC的中點(diǎn),在這個(gè)正四面體中,
①GH與EF平行;②BD與MN為異面直線;③GH與MN成60°角;④DE與MN垂直.以上四個(gè)命題中,正確命題的序號(hào)是 . 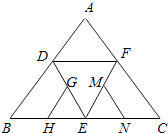
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)![]() ,
, ![]() .
.
(1) 關(guān)于![]() 的方程
的方程![]() 在區(qū)間
在區(qū)間![]() 上有解,求
上有解,求![]() 的取值范圍;
的取值范圍;
(2) 當(dāng)![]() 時(shí),
時(shí), ![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】用數(shù)學(xué)歸納法證明12+22+…+(n﹣1)2+n2+(n﹣1)2+…+22+12═ ![]() 時(shí),由n=k的假設(shè)到證明n=k+1時(shí),等式左邊應(yīng)添加的式子是( )
時(shí),由n=k的假設(shè)到證明n=k+1時(shí),等式左邊應(yīng)添加的式子是( )
A.(k+1)2+2k2
B.(k+1)2+k2
C.(k+1)2
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在三棱錐S﹣ABC中,G1 , G2分別是△SAB和△SAC的重心,則直線G1G2與BC的位置關(guān)系是( ) 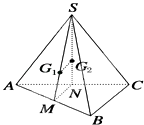
A.相交
B.平行
C.異面
D.以上都有可能
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為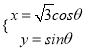 (
(![]() 為參數(shù)),以坐標(biāo)原點(diǎn)
為參數(shù)),以坐標(biāo)原點(diǎn)![]() 為極點(diǎn),以
為極點(diǎn),以![]() 軸正半軸為極軸,建立極坐標(biāo)系,曲線
軸正半軸為極軸,建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)寫(xiě)出![]() 的普通方程和
的普通方程和![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)點(diǎn)![]() 在
在![]() 上,點(diǎn)
上,點(diǎn)![]() 在
在![]() 上,求
上,求![]() 的最小值及此時(shí)
的最小值及此時(shí)![]() 的直角坐標(biāo).
的直角坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,正方形![]() ,直角梯形
,直角梯形![]() ,直角梯形
,直角梯形![]() 所在平面兩兩垂直,
所在平面兩兩垂直, ![]() ,且
,且![]() ,
, ![]() .
.
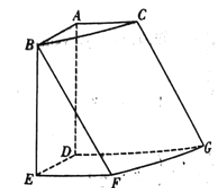
(1)求證: ![]() 四點(diǎn)共面;
四點(diǎn)共面;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知以點(diǎn)C(t, ![]() )(t∈R,t≠0)為圓心的圓過(guò)原點(diǎn)O.
)(t∈R,t≠0)為圓心的圓過(guò)原點(diǎn)O.
(1)設(shè)直線3x+y﹣4=0與圓C交于點(diǎn)M,N,若|OM|=|ON|,求圓C的方程;
(2)在(1)的條件下,設(shè)B(0,2),且P,Q分別是直線l:x+y+2=0和圓C上的動(dòng)點(diǎn),求|PQ|﹣|PB|的最大值及此時(shí)點(diǎn)P的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知△ABC的三個(gè)內(nèi)角A,B,C所對(duì)的邊分別為a,b,c,若三個(gè)內(nèi)角A,B,C成等差數(shù)列,且a= ![]() ,b=
,b= ![]() ,求sinC的值.
,求sinC的值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com