Question

【題目】已知函數(shù)關(guān)于x的函數(shù).

（1）當(dāng)時，求的值域；

（2）若不等式對恒成立，求實數(shù)m的取值范圍；

（3）若函數(shù)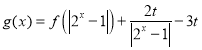有3個零點，求實數(shù)t的取值范圍.

Answer 1

【答案】（1）（2）（3）

【解析】

（1）首先根據(jù)對勾函數(shù)的單調(diào)性得到的單調(diào)性，結(jié)合定義域即可得值域；

（2）利用分離參數(shù)思想得出恒成立，求不等式右邊的最小值即可；

（3）設(shè)，換元轉(zhuǎn)化為方程的根的范圍問題，再用根的分布方法求解.

（1）函數(shù)在上單調(diào)遞減，在上單調(diào)遞增；

又，；

故的值域為；

（2）不等式對恒成立；

即，則；

∵，∴

故實數(shù)m的取值范圍：；

（3）根據(jù)題意有，則；

設(shè)，則；

由條件有3個零點，則

即方程有兩個不等實數(shù)根；

且兩個根，滿足：，；

設(shè)函數(shù)

當(dāng)時，，此時不滿足條件；

∴，則；

故實數(shù)t的取值范圍：.