Question

【題目】若對任意的正整數，總存在正整數，使得數列的前項和，則稱是“回歸數列”.

（1）①前項和為的數列是否是“回歸數列”?并請說明理由；

②通項公式為的數列是否是“回歸數列”?并請說明理由；

（2）設是等差數列，首項，公差，若是“回歸數列”，求的值；

（3）是否對任意的等差數列，總存在兩個“回歸數列”和，使得成立，請給出你的結論，并說明理由.

Answer 1

【答案】（1）①是；②是；（2）；（3）見解析.

【解析】

（1）①利用公式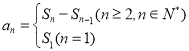和 ，求出數列的通項公式，按照回歸數列的定義進行判斷；

②求出數列的前項和，按照回歸數列的定義進行判斷；

（2）求出的前項和，根據是“回歸數列”，可得到等式，通過取特殊值，求出的值；

（3）等差數列的公差為，構造數列，可證明

、是等差數列，再利用等差數列前項和，及其通項公式，回歸數列的概念，即可求出.

（1）①當時，，

當時，，當時，，，所以數列是“回歸數列”；

②因為，所以前n項和，根據題意，

因為一定是偶數，所以存在，使得，

所以數列{}是“回歸數列”；

（2）設是等差數列為，由題意可知：對任意的正整數，總存在正整數，使得數列的前項和，即，取，得，解得，公差，所以，又；

（3）設等差數列=，

總存在兩個回歸數列，顯然和是等差數列，使得，

證明如下：，

數列{}前n項和，

時，為正整數，當時，，

所以存在正整數，使得，所以{}是“回歸數列”，

數列{}前n項和，存在正整數，使得，所以{}是“回歸數列”，所以結論成立.