
【題目】設(shè)橢圓M:![]()
![]() 的離心率與雙曲線
的離心率與雙曲線![]() 的離心率互為倒數(shù),且內(nèi)切于圓
的離心率互為倒數(shù),且內(nèi)切于圓![]() 。
。
(1)求橢圓M的方程;
(2)已知![]() ,
,![]() 是橢圓M的下焦點(diǎn),在橢圓M上是否存在點(diǎn)P,使
是橢圓M的下焦點(diǎn),在橢圓M上是否存在點(diǎn)P,使![]() 的周長最大?若存在,請(qǐng)求出
的周長最大?若存在,請(qǐng)求出![]() 周長的最大值,并求此時(shí)
周長的最大值,并求此時(shí)![]() 的面積;若不存在,請(qǐng)說明理由。
的面積;若不存在,請(qǐng)說明理由。
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)雙曲線的離心率為![]() ,∴橢圓的離心率為
,∴橢圓的離心率為![]()
∵橢圓M內(nèi)切于圓![]()
![]() 得解。
得解。
(2)橢圓的焦點(diǎn)為![]() ,由橢圓的定義得:
,由橢圓的定義得:![]()
![]() 的周長為
的周長為![]()
當(dāng)且僅當(dāng)點(diǎn)P在線段![]() 的延長線上時(shí)取等號(hào)。
的延長線上時(shí)取等號(hào)。
∴在橢圓M上存在點(diǎn)P,使![]() 的周長取得最大值
的周長取得最大值![]() ,
,
直線![]() 的方程為
的方程為![]() ,由 ∵點(diǎn)P在線段
,由 ∵點(diǎn)P在線段![]() 的延長線上,∴點(diǎn)P的坐標(biāo)為
的延長線上,∴點(diǎn)P的坐標(biāo)為![]() ,再求解
,再求解![]() 的面積。
的面積。
(1)∵雙曲線![]() 的離心率為
的離心率為![]() ,∴橢圓M的離心率為
,∴橢圓M的離心率為![]()
∵橢圓M內(nèi)切于圓![]()
![]()
得: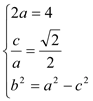
![]()
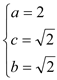 所求橢圓M的方程為
所求橢圓M的方程為![]() .
.
(2)橢圓M的上焦點(diǎn)為![]() ,由橢圓的定義得:
,由橢圓的定義得:![]()
![]() 的周長為
的周長為![]()
當(dāng)且僅當(dāng)點(diǎn)P在線段![]() 的延長線上時(shí)取等號(hào)。
的延長線上時(shí)取等號(hào)。
∴在橢圓M上存在點(diǎn)P,使![]() 的周長取得最大值
的周長取得最大值![]() ,
,
直線![]() 的方程為
的方程為![]() ,由
,由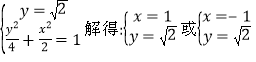
∵點(diǎn)P在線段![]() 的延長線上,∴點(diǎn)P的坐標(biāo)為
的延長線上,∴點(diǎn)P的坐標(biāo)為![]() ,
,
![]() 的面積
的面積![]() 。
。



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對(duì)于函數(shù)f(x),若存在區(qū)間M=[a,b](a<b)使得{y|y=f(x),x∈M}=M,則稱區(qū)間M為函數(shù)f(x)的一個(gè)“穩(wěn)定區(qū)間,給出下列四個(gè)函數(shù):
①f(x)![]() ,②f(x)=x3,③f(x)=cos
,②f(x)=x3,③f(x)=cos![]() x,④f(x)=tanx
x,④f(x)=tanx
其中存在“穩(wěn)定區(qū)間”的函數(shù)有( )
A.①②③B.②③C.③④D.①④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,一個(gè)正方形花圃被分成5份.

(1)若給這5個(gè)部分種植花,要求相鄰兩部分種植不同顏色的花,己知現(xiàn)有紅、黃、藍(lán)、綠4種顏色不同的花,求有多少種不同的種植方法?
(2)若向這5個(gè)部分放入7個(gè)不同的盆栽,要求每個(gè)部分都有盆栽,問有多少種不同的放法?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校有微機(jī)![]() 臺(tái),分別放在
臺(tái),分別放在![]() 個(gè)房間,各房間開門鑰匙互不相同.某期培訓(xùn)班有學(xué)員
個(gè)房間,各房間開門鑰匙互不相同.某期培訓(xùn)班有學(xué)員![]() 人(
人(![]() ),每晚恰有
),每晚恰有![]() 人進(jìn)機(jī)房實(shí)習(xí)操作,為保證每人一臺(tái)機(jī),至少應(yīng)準(zhǔn)備多少把鑰匙分給這
人進(jìn)機(jī)房實(shí)習(xí)操作,為保證每人一臺(tái)機(jī),至少應(yīng)準(zhǔn)備多少把鑰匙分給這![]() 個(gè)學(xué)員,使得每晚不論哪
個(gè)學(xué)員,使得每晚不論哪![]() 個(gè)人進(jìn)機(jī)房,都能用自己分到的鑰匙打開一間機(jī)房的門進(jìn)去練習(xí),并按分得鑰匙少的人先開門的原則,能保證每人恰可得到一個(gè)房間.
個(gè)人進(jìn)機(jī)房,都能用自己分到的鑰匙打開一間機(jī)房的門進(jìn)去練習(xí),并按分得鑰匙少的人先開門的原則,能保證每人恰可得到一個(gè)房間.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】考慮某長方體的三個(gè)兩兩相鄰的面上的三條對(duì)角線及體對(duì)角線(共四條線段),則正確的命題是( )
A. 必有某三條線段不能組成一個(gè)三角形的三邊
B. 任何三條線段都可組成三角形,其每個(gè)內(nèi)角都是銳角
C. 任何三條線段都可組成三角形,其中必有一個(gè)是鈍角三角形
D. 任何三條線段都可組成三角形,其形狀是“銳角的”或是“非銳角的”,隨長方體的長、寬、高而變化,不能確定
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD為直角梯形,BC∥AD,AB⊥BC,∠ADC=45°,PA⊥平面ABCD,AB=AP=1,AD=3.
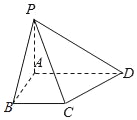
(1)求異面直線PB與CD所成角的大小;
(2)求點(diǎn)D到平面PBC的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,已知圓
中,已知圓![]() 的方程為
的方程為![]() ,過點(diǎn)
,過點(diǎn)![]() 的直線
的直線![]() 與圓
與圓![]() 交于兩點(diǎn)
交于兩點(diǎn)![]() ,
,![]() .
.
(1)若![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)若直線![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,設(shè)
,設(shè)![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() 與圓
與圓![]() .
.
(1)求證兩圓相交;
(2)求兩圓公共弦所在直線的方程;
(3)求過兩圓的交點(diǎn)且圓心在直線![]() 上的圓的方程.
上的圓的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題14分)設(shè)![]() ,
, ![]() .
.
(1)當(dāng)![]() 時(shí),求曲線
時(shí),求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)如果存在![]() ,使得
,使得![]() 成立,
成立,
求滿足上述條件的最大整數(shù)![]() ;
;
(3)如果對(duì)任意的![]() ,都有
,都有![]() 成立,求實(shí)數(shù)
成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com