【題目】設(shè)雙曲線
的兩支為
(如圖)，正三角形PQR的三頂點位于此雙曲線上。
（1）求證：P、Q、R不能都在雙曲線的同一支上；
（2）設(shè)P(-1，-1)在
上，Q、R在
上。求頂點Q、R的坐標(biāo)。
【答案】（1）見解析；（2）
，
【解析】
(1)用反證法.
假設(shè)正△PQR的三頂點P、Q、R位于同一支如
上，其坐示分別的
，不妨設(shè)0
.則一定有
.于是，
.
因此
.
這說明△PQR是鈍角三角形，與△PQR為正三角形矛盾.故P、Q、R不能位于同一支上.
(2)設(shè)Q、R的坐標(biāo)為
，這時QR邊上的高線方程為
.
它必過線段QR的中點，因此QR的中點坐標(biāo)滿足方程(1)，
于是有
.此即 
..
，上式方括號中的式子明顯大于0，則
.故
.
于是，Q的坐標(biāo)為
.而R的坐標(biāo)為
，這說明Q、R關(guān)于直線y=x對稱.
PQ、PR所在的直線分別為過P點與y=x交成30°角的相互對稱的兩條直線，易見其傾斜角分別為75°和15°.不妨設(shè)PQ的傾斜角為75°，這時它的方程為
即 
.將其代入雙曲線方程
，解得Q的坐標(biāo)為
，由對稱性知R的坐標(biāo)為
.
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在平面直角坐標(biāo)系
中，圓
，把圓
上每一點的橫坐標(biāo)伸長為原來的2倍，縱坐標(biāo)不變，得到曲線
，且傾斜角為
，經(jīng)過點
的直線
與曲線
交于
兩點.
（1）當(dāng)
時，求曲線
的普通方程與直線
的參數(shù)方程；
（2）求點
到
兩點的距離之積的最小值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】選修4—4：坐標(biāo)系與參數(shù)方程
點P是曲線C1:(x-2)2+y2=4上的動點,以坐標(biāo)原點O為極點,x軸的正半軸為極軸
建立極坐標(biāo)系,將點P繞極點O逆時針90得到點Q,設(shè)點Q的軌跡為曲線C2.
求曲線C1,C2的極坐標(biāo)方程;
射線=
(>0)與曲線C1,C2分別交于A,B兩點,定點M(2,0),求MAB的面積
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
的離心率為
，且經(jīng)過點P
，過它的左、右焦點
分別作直線l1和12.l1交橢圓于A.兩點，l2交橢圓于C,D兩點， 且
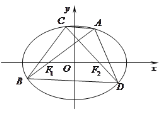
(1)求橢圓的標(biāo)準(zhǔn)方程.
(2)求四邊形ACBD的面積S的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在平面直角坐標(biāo)系
中，設(shè)拋物線
的焦點是雙曲線
的右焦點，拋物線的準(zhǔn)線與
軸的交點為
，若拋物線上存在一點
，且
，則直線
的方程為__________．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】游樂場的摩天輪勻速旋轉(zhuǎn)，其中心O距地面40.5m，半徑40m.若從最低點處登上座天輪，那么人與地面的距離將隨時間變化，5min后達(dá)到最高點，在你登上摩天輪時開始計時，
（1）求出人與地面距離y與時間t的函數(shù)解析式；
（2）從登上摩天輪到旋轉(zhuǎn)一周過程中，有多長時間人與地面距離大于20.5m.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某地區(qū)某農(nóng)產(chǎn)品近幾年的產(chǎn)量統(tǒng)計如表：
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代碼t | 1 | 2 | 3 | 4 | 5 | 6 |
年產(chǎn)量y(萬噸) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
（Ⅰ）根據(jù)表中數(shù)據(jù)，建立
關(guān)于的線性回歸方程
；
（Ⅱ）根據(jù)線性回歸方程預(yù)測2019年該地區(qū)該農(nóng)產(chǎn)品的年產(chǎn)量.
附:對于一組數(shù)據(jù)
，其回歸直線的斜率和截距的最小二乘估計分別為：
，
.(參考數(shù)據(jù):
，計算結(jié)果保留小數(shù)點后兩位）
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
