
【題目】如圖,在直角梯形![]() 中,
中,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 分別在線段
分別在線段![]() 和
和![]() 上,且
上,且![]() ,
,![]() 是等腰直角三角形.
是等腰直角三角形.
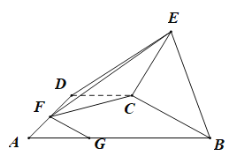
(1)若![]() ,求證:
,求證:![]() 平面
平面![]() .
.
(2)![]() ,是否存在
,是否存在![]() ,使得
,使得![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】(1)證明見解析;(2)存在,![]()
【解析】
(1)根據題意分析可得![]() 是等腰三角形,可得
是等腰三角形,可得![]() ,進而可得
,進而可得![]() ,進而可得
,進而可得![]() ,即可得到結論;
,即可得到結論;
(2)根據題意,建立空間直角坐標系,得![]() ,
,![]() ,
,![]() ,進而可得平面
,進而可得平面![]() 的一個法向量,再利用
的一個法向量,再利用![]() ,得方程
,得方程![]() 解得即可得到結論.
解得即可得到結論.
(1)連接![]() ,
,![]() ,
,![]() .
.
又![]() 是等腰三角形,
是等腰三角形,![]() .
.
在直角梯形![]() 中,
中,![]() ,故
,故![]() 為直角三角形,
為直角三角形,
在![]() 中,
中,![]() ,
,
![]() ,
,![]() ,
,![]() 在
在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() ,故
,故![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
(2)如圖,過![]() 作
作![]() 且
且![]() ,連接
,連接![]() 得四邊形
得四邊形![]() 為矩形.以
為矩形.以![]() 為原點,
為原點,![]() ,
,![]() 的方向為
的方向為![]() 軸,
軸,![]() 軸的正方向建立如圖所示空間直角坐標系
軸的正方向建立如圖所示空間直角坐標系![]() ,
,
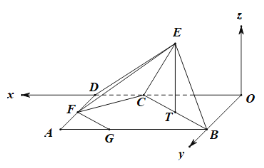
則![]() ,
,![]() ,
,![]() .
.
設![]() 的中點為
的中點為![]() ,連接
,連接![]() ,
,
![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
設平面![]() 的一個法向量為
的一個法向量為![]() ,
,
則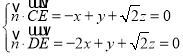
令![]() ,得
,得![]() .
.
設![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,
,
則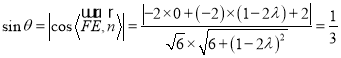 ,
,
化簡得![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
![]() 存在實數
存在實數![]() ,使得
,使得![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]() ,此時
,此時![]() .
.


科目:高中數學 來源: 題型:
【題目】2019年春節前后,中國爆發新型冠狀病毒(SARS-Cov-2)如圖所示為1月24日至2月16日中國內地(除湖北以外的)感染新型冠狀病毒新增人數的折線圖,為了預測分析數據的變化規律,建立了![]() 與時間變量
與時間變量![]() 的不同時間段的兩個線性回歸模型.根據1月24日至2月3日的數據(時間變量
的不同時間段的兩個線性回歸模型.根據1月24日至2月3日的數據(時間變量![]() 的值依次為1,2,3,4,5,6,7,8,9,10,11)建立模型①:
的值依次為1,2,3,4,5,6,7,8,9,10,11)建立模型①:![]() ;根據2月4日至2月16日的數據(時間變量
;根據2月4日至2月16日的數據(時間變量![]() 的值依次為12,13,14,15,16,17,18,19,20,21,22,23,24)建立模型②:
的值依次為12,13,14,15,16,17,18,19,20,21,22,23,24)建立模型②:![]() .
.
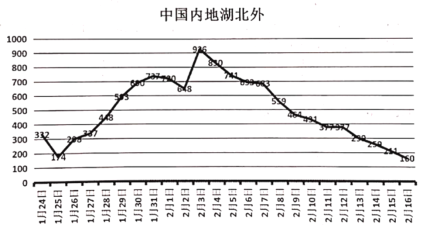
1月 24日 | 1月 25日 | 1月 26日 | 1月 27日 | 1月 28日 | 1月 29日 | 1月 30日 | 1月 31日 | 2月 1日 | 2月 2日 | 2月 3日 |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
332 | 174 | 298 | 337 | 448 | 593 | 690 | 737 | 720 | 648 | 926 |
2月 4日 | 2月 5日 | 2月 6日 | 2月 7日 | 2月 8日 | 2月 9日 | 2月 10日 | 2月 11日 | 2月 12日 | 2月 13日 | 2月 14日 | 2月 15日 | 2月 16日 |
12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
830 | 741 | 693 | 683 | 559 | 464 | 431 | 377 | 377 | 299 | 259 | 211 | 160 |
(1)求出兩個回歸直線方程;(計算結果取整數)
(2)中國政府為了人民的生命安全,聽取專家意見,了解了病毒信息,并迅速做出一系列的隔離防護措施,但新冠狀病毒在世界范圍內爆發時,某些歐美國家采取放任的態度,不治療、不隔離、不檢測,甚至不公布,請你用以上數據說明采取一系列措施的必要性,不采取措施的后果.
參考數據:![]() ,
,![]() ,
,![]() ,
,![]()
參考公式: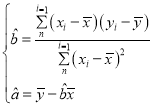 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C:y2=2px的焦點為F,過點F且斜率為1的直線l截得圓:x2+y2=p2的弦長為2![]() .
.
(1)求拋物線C的方程;
(2)若過點F作互相垂直的兩條直線l1、l2,l1與拋物線C交于A、B兩點,l2與拋物線C交于D、E兩點,M、N分別為弦AB、DE的中點,求|MF||NF|的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“柯西不等式”是由數學家柯西在研究數學分析中的“流數”問題時得到的,但從歷史的角度講,該不等式應當稱為柯西﹣﹣布尼亞科夫斯基﹣﹣施瓦茨不等式,因為正是后兩位數學家彼此獨立地在積分學中推而廣之,才將這一不等式推廣到完善的地步,在高中數學選修教材4﹣5中給出了二維形式的柯西不等式:(a2+b2)(c2+d2)≥(ac+bd)2當且僅當ad=bc(即![]() )時等號成立.該不等式在數學中證明不等式和求函數最值等方面都有廣泛的應用.根據柯西不等式可知函數
)時等號成立.該不等式在數學中證明不等式和求函數最值等方面都有廣泛的應用.根據柯西不等式可知函數![]() 的最大值及取得最大值時x的值分別為( )
的最大值及取得最大值時x的值分別為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在棱長為1的正方體![]() 中,E,F分別為線段CD和
中,E,F分別為線段CD和![]() 上的動點,且滿足
上的動點,且滿足![]() ,則四邊形
,則四邊形![]() 所圍成的圖形(如圖所示陰影部分)分別在該正方體有公共頂點的三個面上的正投影的面積之和( )
所圍成的圖形(如圖所示陰影部分)分別在該正方體有公共頂點的三個面上的正投影的面積之和( )

A. 有最小值![]() B. 有最大值
B. 有最大值![]() C. 為定值3D. 為定值2
C. 為定值3D. 為定值2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】干支歷法是上古文明的產物,又稱節氣歷或中國陽歷,是一部深奧的歷法.它是用60組各不相同的天干地支標記年月日時的歷法.具體的算法如下:先用年份的尾數查出天干,如2013年3為癸;再用2013年除以12余數為9,9為巳.那么2013年就是癸巳年了,
天干 | 甲 | 乙 | 丙 | 丁 | 戊 | 己 | 庚 | 辛 | 壬 | 癸 | ||
4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 | |||
地支 | 子 | 丑 | 寅 | 卯 | 辰 | 巳 | 午 | 未 | 申 | 酉 | 戌 | 亥 |
4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 1 | 2 | 3 |
2020年高三應屆畢業生李東是壬午年出生,李東的父親比他大25歲.問李東的父親是哪一年出生( )
A.甲子B.乙丑C.丁巳D.丙卯
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在極坐標系中曲線C的極坐標方程為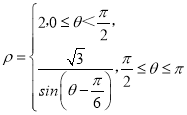 .
.
(1)求曲線C與極軸所在直線圍成圖形的面積;
(2)設曲線C與曲線ρsinθ=1交于A,B,求|AB|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() .
.
(1)討論![]() 時,
時,![]() 的單調性、極值;
的單調性、極值;
(2)求證:在(1)的條件下,![]() ;
;
(3)是否存在實數a,使![]() 的最小值是3,如果存在,求出a的值;若不存在,
的最小值是3,如果存在,求出a的值;若不存在,
請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com