
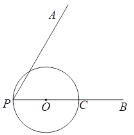
【題目】如圖,∠APB,點(diǎn)C在射線PB上,PC為⊙O的直徑,在∠APB內(nèi)部且到∠APB兩邊距離都相等的所有的點(diǎn)組成圖形M,圖形M交⊙O于D,過(guò)點(diǎn)D作直線DE⊥PA,分別交射線PA,PB于E,F.
(1)根據(jù)題意補(bǔ)全圖形;
(2)求證:DE是⊙O的切線;
(3)如果PC=2CF,且![]() ,求PE的長(zhǎng).
,求PE的長(zhǎng).
【答案】(1)作圖見(jiàn)解析;(2)證明見(jiàn)解析;(3)![]() .
.
【解析】
(1)根據(jù)題目要求畫(huà)出圖形即可得到.
(2)連接OD,利用角平分線的性質(zhì)以及平行的性質(zhì)證明DE⊥OD,即可證明DE是⊙O的切線.
(3)先證明OF=2OD,推出∠OFD=30°,解直角三角形求出OD,OF,PF即可解決問(wèn)題.
解:(1)如圖所示,補(bǔ)全圖形

(2)證明:連接OD.
∵DE⊥PA,
∴∠PED=90°.
∵依題意,PD是∠APB的角平分線,
∴∠APD=∠DPB.
∵OP=OD,
∴∠DPB =∠PDO.
∴∠APD=∠PDO.
∴AP∥OD,
∴∠ODF=∠PED=90°,
∴DE是⊙O的切線.
(3)∵PC=2CF,
∴設(shè)CF=x,那么PC=2x,OD=x.
∵∠ODF=90°,
∴在Rt△ODF中,OD=![]() .
.
又∵![]() ,
,
∴OD=1,OF=2,PF=3.
∵在Rt△PEF中,∠PEF=90°,
∴![]() .
.
∴![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
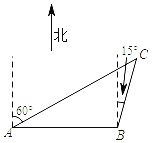
【題目】在一次綜合社會(huì)實(shí)踐活動(dòng)中,小東同學(xué)從A處出發(fā),要到A地北偏東60°方向的C處,他先沿正東方向走了4千米到達(dá)B處,再沿北偏東15°方向走,恰能到達(dá)目的地C,如圖所示,則A、C兩地相距__千米.(結(jié)果精確到0.1千米,參考數(shù)據(jù):![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
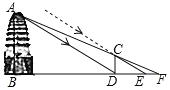
【題目】如圖,西安市薦福寺內(nèi)的小雁塔,是中國(guó)早期方形密檐式磚塔的典型作品,并作為絲綢之路的一處重要遺址點(diǎn),被列入《世界遺產(chǎn)名錄》.某周末,小樂(lè)和小夏相約去小雁塔游玩,在休息時(shí),他們想利用所學(xué)知識(shí)測(cè)量小雁塔的高度,于是他們向工作人員借來(lái)測(cè)量工具由于觀測(cè)點(diǎn)與小雁塔底部間的距離不易測(cè)量,于是他們利用太陽(yáng)光照射影子進(jìn)行測(cè)量,小樂(lè)先在小雁塔的影子頂端![]() 處豎直立一根長(zhǎng)1.72米的木棒
處豎直立一根長(zhǎng)1.72米的木棒![]() ,并測(cè)得此時(shí)木棒的影長(zhǎng)
,并測(cè)得此時(shí)木棒的影長(zhǎng)![]() 米;然后小夏在
米;然后小夏在![]() 的延長(zhǎng)線上找出一點(diǎn)
的延長(zhǎng)線上找出一點(diǎn)![]() ,使得
,使得![]() 、
、![]() 、
、![]() 三點(diǎn)在同一直線上,并測(cè)得
三點(diǎn)在同一直線上,并測(cè)得![]() 米已知圖中所有點(diǎn)均在同一平面內(nèi),
米已知圖中所有點(diǎn)均在同一平面內(nèi),![]() ,
,![]() ,根據(jù)以上測(cè)量過(guò)程及數(shù)據(jù),請(qǐng)你幫他們求出小雁塔的高度
,根據(jù)以上測(cè)量過(guò)程及數(shù)據(jù),請(qǐng)你幫他們求出小雁塔的高度![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,一次函數(shù)y=kx+b(k≠0)的圖象與反比例函數(shù)y=![]() (m≠0,x>0)的圖象在第一象限內(nèi)交于點(diǎn)A,B,且該一次函數(shù)的圖象與y軸正半軸交于點(diǎn)C,過(guò)A,B分別作y軸的垂線,垂足分別為D,E.已知A(1,4),
(m≠0,x>0)的圖象在第一象限內(nèi)交于點(diǎn)A,B,且該一次函數(shù)的圖象與y軸正半軸交于點(diǎn)C,過(guò)A,B分別作y軸的垂線,垂足分別為D,E.已知A(1,4),![]() =
=![]() .
.
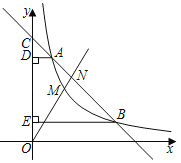
(1)求m的值和一次函數(shù)的解析式;
(2)若點(diǎn)M為反比例函數(shù)圖象在A,B之間的動(dòng)點(diǎn),作射線OM交直線AB于點(diǎn)N,當(dāng)MN長(zhǎng)度最大時(shí),直接寫(xiě)出點(diǎn)M的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知,如圖,在菱形ABCD中.(1)分別以C,D為圓心,大于![]() 長(zhǎng)為半徑作弧,兩弧分別交于點(diǎn)E,F;(2)作直線EF,且直線EF恰好經(jīng)過(guò)點(diǎn)A,且與邊CD交于點(diǎn)M;(3)連接BM.根據(jù)以上作圖過(guò)程及所作圖形,判斷下列結(jié)論中錯(cuò)誤的是( )
長(zhǎng)為半徑作弧,兩弧分別交于點(diǎn)E,F;(2)作直線EF,且直線EF恰好經(jīng)過(guò)點(diǎn)A,且與邊CD交于點(diǎn)M;(3)連接BM.根據(jù)以上作圖過(guò)程及所作圖形,判斷下列結(jié)論中錯(cuò)誤的是( )

A.∠ABC=60°B.如果AB=2,那么BM=4
C.BC=2CMD.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
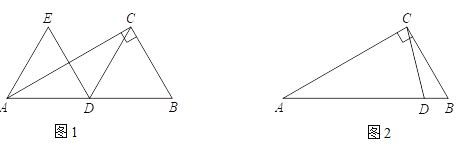
【題目】在△ABC中,∠ACB=90°,∠CAB=30°,點(diǎn)D在AB上,連接CD,并將CD繞點(diǎn)D逆時(shí)針旋轉(zhuǎn)60°得到DE,連接AE.
(1)如圖1,當(dāng)點(diǎn)D為AB中點(diǎn)時(shí),直接寫(xiě)出DE與AE長(zhǎng)度之間的數(shù)量關(guān)系;
(2)如圖2,當(dāng)點(diǎn)D在線段AB上時(shí),
① 根據(jù)題意補(bǔ)全圖2;
② 猜想DE與AE長(zhǎng)度之間的數(shù)量關(guān)系,并證明.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 的圖象與反比例函數(shù)
的圖象與反比例函數(shù)![]() 的圖象交于點(diǎn)
的圖象交于點(diǎn)![]() .
.

(1)求![]() 、
、![]() 的值;
的值;
(2)點(diǎn)![]() 是
是![]() 軸上的一點(diǎn),過(guò)點(diǎn)
軸上的一點(diǎn),過(guò)點(diǎn)![]() 作
作![]() 軸的垂線,交直線
軸的垂線,交直線![]() 于點(diǎn)
于點(diǎn)![]() ,交反比例函數(shù)
,交反比例函數(shù)![]() 的圖象于點(diǎn)
的圖象于點(diǎn)![]() .橫、縱坐標(biāo)都是整數(shù)的點(diǎn)叫做整點(diǎn).記
.橫、縱坐標(biāo)都是整數(shù)的點(diǎn)叫做整點(diǎn).記![]() 的圖象在點(diǎn)
的圖象在點(diǎn)![]() ,
,![]() 之間的部分與線段
之間的部分與線段![]() ,
,![]() 圍成的區(qū)域(不含邊界)為
圍成的區(qū)域(不含邊界)為![]() .
.
①當(dāng)![]() 時(shí),直接寫(xiě)出區(qū)域
時(shí),直接寫(xiě)出區(qū)域![]() 內(nèi)的整點(diǎn)的坐標(biāo)為______;
內(nèi)的整點(diǎn)的坐標(biāo)為______;
②若區(qū)域![]() 內(nèi)恰有6個(gè)整點(diǎn),結(jié)合函數(shù)圖象,求出
內(nèi)恰有6個(gè)整點(diǎn),結(jié)合函數(shù)圖象,求出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知線段![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 的射線
的射線![]() .在射線
.在射線![]() 上截取線段
上截取線段![]() ,連接
,連接![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 為
為![]() 邊上一動(dòng)點(diǎn),點(diǎn)
邊上一動(dòng)點(diǎn),點(diǎn)![]() 為線段
為線段![]() 上一動(dòng)點(diǎn).以點(diǎn)
上一動(dòng)點(diǎn).以點(diǎn)![]() 為旋轉(zhuǎn)中心,將
為旋轉(zhuǎn)中心,將![]() 逆時(shí)針旋轉(zhuǎn)
逆時(shí)針旋轉(zhuǎn)![]() 得到
得到![]() 的對(duì)應(yīng)點(diǎn)為
的對(duì)應(yīng)點(diǎn)為![]() 的對(duì)應(yīng)點(diǎn)為
的對(duì)應(yīng)點(diǎn)為![]() .
.
(1)當(dāng)點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 重合,且點(diǎn)
重合,且點(diǎn)![]() 不是
不是![]() 中點(diǎn)時(shí),
中點(diǎn)時(shí),
①據(jù)題意在圖中補(bǔ)全圖形;
②證明:以![]() 為頂點(diǎn)的四邊形是矩形.
為頂點(diǎn)的四邊形是矩形.
(2)連接![]() ,若
,若![]() ,從下列3個(gè)條件中選擇1個(gè):
,從下列3個(gè)條件中選擇1個(gè):
①![]() ,②
,②![]() ,③
,③![]() ,
,
當(dāng)條件______(填入序號(hào))滿足時(shí),一定有![]() ,并證明這個(gè)結(jié)論.
,并證明這個(gè)結(jié)論.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知直線l及直線l外一點(diǎn)P.如圖,
(1)在直線l上取一點(diǎn)A,連接PA;
(2)作PA的垂直平分線MN,分別交直線l,PA于點(diǎn)B,O;
(3)以O為圓心,OB長(zhǎng)為半徑畫(huà)弧,交直線MN于另一點(diǎn)Q;
(4)作直線PQ.
根據(jù)以上作圖過(guò)程及所作圖形,下列結(jié)論中錯(cuò)誤的是( )
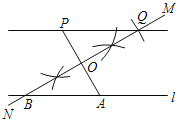
A.△OPQ≌△OABB.PQ∥AB
C.AP=![]() BQD.若PQ=PA,則∠APQ=60°
BQD.若PQ=PA,則∠APQ=60°
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com