
【題目】在平面直角坐標(biāo)系![]() 中,拋物線
中,拋物線![]() 與x軸交于A、B兩點,與軸交于點
與x軸交于A、B兩點,與軸交于點![]() ,連接
,連接![]() 、
、![]() .
.
(1)求拋物線的函數(shù)表達式;
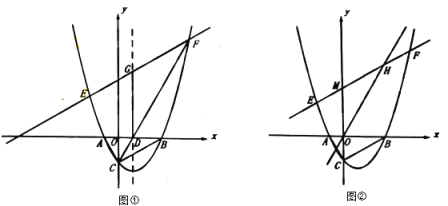
(2)拋物線的對稱軸與x軸交于點D,連接![]() ,點E為第三象限拋物線上的一動點,
,點E為第三象限拋物線上的一動點,![]() ,直線
,直線![]() 與拋物線交于點F,設(shè)直線
與拋物線交于點F,設(shè)直線![]() 的表達式為
的表達式為![]() .
.
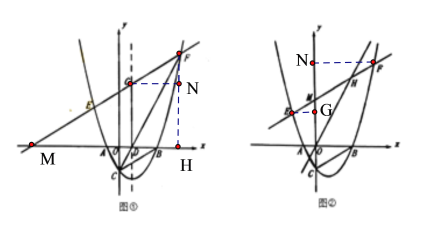
①如圖①,直線![]() 與拋物線對稱軸交于點G,若
與拋物線對稱軸交于點G,若![]() ,求k、b的值;
,求k、b的值;
②如圖②,直線![]() 與y軸交于點M,與直線
與y軸交于點M,與直線![]() 交于點H,若
交于點H,若![]() ,求b的值.
,求b的值.
【答案】(1)![]() ;(2)①k=
;(2)①k=![]() ,b=
,b=![]() ,②
,②![]() .
.
【解析】
(1)把![]() 代入
代入![]() ,求出a的值,即可;
,求出a的值,即可;
(2)①由![]() ,DG=FG,由
,DG=FG,由![]() ,∠GMD=∠OBC=30°,過點G作GN∥x軸,過點F作FN∥y軸,交于點N,交x軸于點H,則∠FGN=30°,設(shè)DG=FG=m,得:點F坐標(biāo)是:(1+
,∠GMD=∠OBC=30°,過點G作GN∥x軸,過點F作FN∥y軸,交于點N,交x軸于點H,則∠FGN=30°,設(shè)DG=FG=m,得:點F坐標(biāo)是:(1+![]() ,
,![]() ),代入二次函數(shù)得解析式,可得:點F坐標(biāo)是:(5,
),代入二次函數(shù)得解析式,可得:點F坐標(biāo)是:(5,![]() ),由∠GMD=30°和待定系數(shù)法,分別可得k,b的值;
),由∠GMD=30°和待定系數(shù)法,分別可得k,b的值;
②由直線![]() 與y軸交于點M,與直線
與y軸交于點M,與直線![]() 交于點H,
交于點H,![]() ,可得:
,可得:![]() ,∠EMO=∠OCB=60°,∠HOB=60°,∠MOH=∠MHO=30°,MH=MO=b,作EG⊥y軸,FN⊥y軸,則,ME=
,∠EMO=∠OCB=60°,∠HOB=60°,∠MOH=∠MHO=30°,MH=MO=b,作EG⊥y軸,FN⊥y軸,則,ME=![]() EG,MF=
EG,MF=![]() FN,設(shè)點E,F的很坐標(biāo)分別是:
FN,設(shè)點E,F的很坐標(biāo)分別是:![]() ,
,![]() ,由
,由![]() ,得到關(guān)于b的方程,即可求解.
,得到關(guān)于b的方程,即可求解.
(1)把![]() 代入
代入![]() 得:
得:![]() ,解得:
,解得:![]() ,
,
∴拋物線的函數(shù)表達式為:![]() ;
;
(2)① 由第(1)題,可知:A(-1,0),B(3,0),![]() ,
,
∴OB=3,OC=![]() ,BC=
,BC=![]() =
=![]() ,
,
∴∠OBC=30°,
∵拋物線的對稱軸與x軸交于點D,
∴D坐標(biāo)為(1,0),即OD=1,BD=2,
∴CD=![]() ,
,
∴BD=CD,
∵![]() ,
,
∴DG=FG,
∵![]() ,
,
∴∠GMD=∠OBC=30°,
過點G作GN∥x軸,過點F作FN∥y軸,交于點N,交x軸于點H,則∠FGN=30°,如圖①,
設(shè)DG=FG=m,則![]() ,
,![]() ,
,![]() ,
,
∴FH=FN+NH=![]() ,OH=OD+DH=1+
,OH=OD+DH=1+![]() ,
,
∴點F坐標(biāo)是:(1+![]() ,
,![]() ),
),
∴![]() ,解得:
,解得:![]() ,
,![]() (舍)
(舍)
∴點F坐標(biāo)是:(5,![]() ),
),
∵∠GMD=30°,可設(shè)直線![]() 的表達式為
的表達式為![]() ,
,
把(5,![]() )代入
)代入![]() ,得:
,得:![]() ,解得:b=
,解得:b=![]() ,
,
∴直線![]() 的表達式為:
的表達式為:![]() ,即:k=
,即:k=![]() ,b=
,b=![]() .
.
②∵直線![]() 與y軸交于點M,與直線
與y軸交于點M,與直線![]() 交于點H,
交于點H,![]() ,
,
∴![]() ,∠EMO=∠OCB=60°,∠HOB=60°,∠MOH=∠MHO=30°,
,∠EMO=∠OCB=60°,∠HOB=60°,∠MOH=∠MHO=30°,
∴MH=MO=b,
作EG⊥y軸,FN⊥y軸,則,ME=![]() EG,MF=
EG,MF=![]() FN,
FN,
設(shè)點E,F的很坐標(biāo)分別是:![]() ,
,![]()
聯(lián)立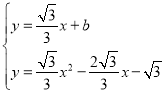 ,得:
,得:![]() ,
,
化簡得:![]() ,
,
∴![]() +
+![]() =3,
=3,![]()
![]() =
=![]() ,
,
∵![]() ,
,
∴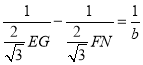 ,即:
,即: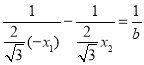 ,
,
化簡得: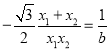 ,
,
∴![]() ,解得:b=
,解得:b=![]()


 通城學(xué)典默寫能手系列答案
通城學(xué)典默寫能手系列答案 金牌教輔培優(yōu)優(yōu)選卷期末沖刺100分系列答案
金牌教輔培優(yōu)優(yōu)選卷期末沖刺100分系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知,在△PAB中,PA=PB,經(jīng)過A、B作⊙O.

(1)如圖1,連接PO,求證:PO平分∠APB;
(2)如圖2,點P在⊙O上,PA:AB=![]() :2,E是⊙O上一點,連接AE、BE.求tan∠AEB的值;
:2,E是⊙O上一點,連接AE、BE.求tan∠AEB的值;
(3)如圖3,在(2)的條件下,AE經(jīng)過圓心O,AE交PB于點F,過F作FG⊥BE于點G,EF+BG=14,求線段OF的長度.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,拋物線![]() 的對稱軸為
的對稱軸為![]() ,與
,與![]() 軸的一個交點在
軸的一個交點在![]() 和
和![]() 之間,其部分圖象如圖所示,則下列結(jié)論:
之間,其部分圖象如圖所示,則下列結(jié)論:
![]() ;
;
![]() ;
;
![]() 點
點![]() 、
、![]() 、
、![]() 是該拋物線上的點,則
是該拋物線上的點,則![]() ;
;
![]() ;
;
![]() (
(![]() 為任意實數(shù)).
為任意實數(shù)).
其中正確結(jié)論的個數(shù)是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
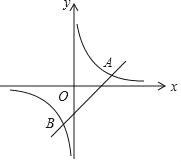
【題目】如圖,已知一次函數(shù)y=x﹣2與反比例函數(shù)y=![]() 的圖象交于A、B兩點.
的圖象交于A、B兩點.
(1)求A、B兩點的坐標(biāo);
(2)觀察圖象,直接寫出一次函數(shù)值小于反比例函數(shù)值的x的取值范圍;
(3)坐標(biāo)原點為O,求△AOB的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
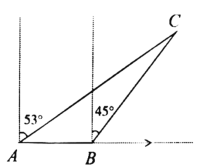
【題目】如圖,漁船跟蹤魚群由西向東航行,到達A處時,測得小島C位于它的北偏東53°方向,再航行![]() 后達到B處(
后達到B處(![]() ),測得小島C位于它的北偏東45°方向.小島C的周圍
),測得小島C位于它的北偏東45°方向.小島C的周圍![]() 內(nèi)有暗礁,如果漁船不改變航向繼續(xù)向東航行,請你通過計算說明漁船有無觸礁的危險?
內(nèi)有暗礁,如果漁船不改變航向繼續(xù)向東航行,請你通過計算說明漁船有無觸礁的危險?
(參考數(shù)據(jù):![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】深圳著名“網(wǎng)紅打卡地”東部華僑城在2018年春節(jié)長假期間,接待游客達20萬人次,預(yù)計在2020年五一長假期間,接待游客獎達28.8萬人次.
一家特色小面店希望在五一長期限期間獲得好的收益,經(jīng)測算知,該小面成本價為每碗6元,借鑒經(jīng)驗:若每碗賣25元,平均每天將銷售3000碗,若價格每降低1元,則平均每天多銷售30碗.
(1)求出2018至2020年五一長假期間游客人次的年平均增長率;
(2)為了更好地維護深圳城市形象,店家規(guī)定每碗售價不得超過20元,則當(dāng)每碗售價定為多少元時,店家才能實現(xiàn)每天利潤6300元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
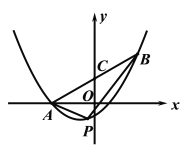
【題目】如圖,拋物線![]() 過點
過點![]() 和點
和點![]() ,連結(jié)AB交y軸于點C.
,連結(jié)AB交y軸于點C.
(1)求拋物線的函數(shù)解析式;
(2)點P在線段AB下方的拋物線上運動,連結(jié)AP,BP. 設(shè)點P的橫坐標(biāo)為m,△ABP的面積為s.
①求s與m的函數(shù)關(guān)系式;
②當(dāng)s取最大值時,拋物線上是否存在點Q,使得S△ACQ=s. 若存在,求點Q的坐標(biāo);若不存在,說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,AB是⊙O 的直徑,CD是⊙O的一條弦,且CD⊥AB于點E.

(1)求證:∠BCO=∠D;
(2)若CD=![]() ,AE=2,求⊙O的半徑.
,AE=2,求⊙O的半徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,拋物線y=ax2-4ax+c(a≠0)與y軸交于點A,將點A向右平移2個單位長度,得到點B.直線![]() 與x軸,y軸分別交于點C,D.
與x軸,y軸分別交于點C,D.
(1)求拋物線的對稱軸.
(2)若點A與點D關(guān)于x軸對稱.
①求點B的坐標(biāo).
②若拋物線與線段BC恰有一個公共點,結(jié)合函數(shù)圖象,求a的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com