
【題目】如果一個正整數(shù)能表示為兩個連續(xù)偶數(shù)的平方差,那么稱這個正整數(shù)為“神秘數(shù)”.
如:![]() ,
,![]() ,
,![]() ,因此
,因此![]() ,
,![]() ,
,![]() 這三個數(shù)都是神秘數(shù).
這三個數(shù)都是神秘數(shù).
(1)![]() 是神秘數(shù)嗎?為什么?
是神秘數(shù)嗎?為什么?
(2)設兩個連續(xù)偶數(shù)為![]() 和
和![]() (其中
(其中![]() 取非負整數(shù)),由這兩個連續(xù)偶數(shù)構造的神秘數(shù)是
取非負整數(shù)),由這兩個連續(xù)偶數(shù)構造的神秘數(shù)是![]() 的倍數(shù)嗎?為什么?
的倍數(shù)嗎?為什么?
(3)①若長方形相鄰兩邊長為兩個連續(xù)偶數(shù),試說明其周長一定為神秘數(shù).
②在①的條件下,面積是否為神秘數(shù)?為什么?
【答案】(1)是,見詳解;(2)是,見詳解;(3)①見詳解,②是,見詳解
【解析】
(1)根據(jù)“神秘數(shù)”的定義,只需看能否把28這個數(shù)寫成兩個連續(xù)偶數(shù)的平方差即可判斷;
(2)運用平方差公式進行計算,進而判斷即可;
(3)①運用周長公式進行計算,進而判斷即可,②運用面積公式進行計算,進而判斷即可.
解:(1)28是“神秘數(shù)”,理由如下:
∵28=82-62,能表示為兩個連續(xù)偶數(shù)的平方差,
∴28是“神秘數(shù)”;
(2)“神秘數(shù)”是4的倍數(shù).理由如下:
∵(2k+2)2-(2k)2=(2k+2+2k)(2k+2-2k)=2(4k+2)=4(2k+1),
∴“神秘數(shù)”是4的倍數(shù);
(3)①設兩個連續(xù)的偶數(shù)為:2k,2k+2(其中![]() 取非負整數(shù)),
取非負整數(shù)),
則周長=![]() ,
,
而由(2)知“神秘數(shù)”可表示為4(2k+1),
∴長方形相鄰兩邊長為兩個連續(xù)偶數(shù),則其周長一定為神秘數(shù).
②長方形的面積=![]() ,
,
∵![]() 取非負整數(shù),
取非負整數(shù),
∴在①的條件下,面積是神秘數(shù).


 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案科目:初中數(shù)學 來源: 題型:
【題目】已知![]() 為
為![]() 直徑,
直徑,![]() 是直徑
是直徑![]() 上一動點(不與點
上一動點(不與點![]() ,
,![]() ,
,![]() 重合),過點
重合),過點![]() 作直線
作直線![]() 交
交![]() 于
于![]() ,
,![]() 兩點,
兩點,![]() 是
是![]() 上一點(不與點
上一點(不與點![]() ,
,![]() 重合),且
重合),且![]() ,直線
,直線![]() 交直線
交直線![]() 于點
于點![]() .
.
![]() 如圖
如圖![]() ,當點
,當點![]() 在線段
在線段![]() 上時,試判斷
上時,試判斷![]() 與
與![]() 的大小關系,并證明你的結論;
的大小關系,并證明你的結論;
![]() 當點
當點![]() 在線段
在線段![]() 上,且
上,且![]() 時,其它條件不變.
時,其它條件不變.

①請你在圖![]() 中畫出符合要求的圖形,并參照圖
中畫出符合要求的圖形,并參照圖![]() 標記字母;
標記字母;
②判斷![]() 中的結論是否還成立,請說明理由.
中的結論是否還成立,請說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,∠AOB=40°,點P在∠AOB的內部,點C,D分別是點P關于直線OA,OB的對稱點,連接CD分別交OA,OB于點E、F.則∠EPF=___________.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,正方形![]() 的邊長為
的邊長為![]() ,
,![]() ,
,![]() 是對角線.將
是對角線.將![]() 繞著點
繞著點![]() 順時針旋轉
順時針旋轉![]() 得到
得到![]() ,
,![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() .則下列結論:
.則下列結論:
①四邊形![]() 是菱形②
是菱形②![]() ③
③![]()
④![]() ,其中正確的結論是( )
,其中正確的結論是( )

A. ①②③④ B. ①②③ C. ①② D. ②
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】(1)如圖矩形![]() 的對角線
的對角線![]() 、
、![]() 交于點
交于點![]() ,過點
,過點![]() 作
作![]() ,且
,且![]() ,連接
,連接![]() ,判斷四邊形
,判斷四邊形![]() 的形狀并說明理由.
的形狀并說明理由.
(2)如果題目中的矩形變?yōu)榱庑危Y論應變?yōu)槭裁矗空f明理由.
(3)如果題目中的矩形變?yōu)檎叫危Y論又應變?yōu)槭裁矗空f明理由.



查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】兩個大小不同的等腰直角三角板按圖①所示的位置放置,圖②是由它抽象畫出的幾何圖形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 在同一條直線上,連接
在同一條直線上,連接![]() .
.
(1)請找出圖②中與![]() 全等的三角形,并給予證明(說明:結論中不得含有未標識的字母);
全等的三角形,并給予證明(說明:結論中不得含有未標識的字母);
(2)求證:![]() .
.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在△ABC中,點D在BC邊上,DE垂直平分AC邊,垂足為點E,若∠B=70°,且AB+BD=BC,則∠BAC的度數(shù)是( )

A.65°B.70°C.75°D.80°
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】尺規(guī)作圖與說理(要求保留作圖痕跡,不寫作法.)如圖,在Rt△ABC中,∠ACB=90°
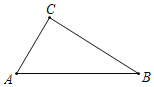
(1)過點C作AB的垂線CD,交AB于點D;
(2)作∠ABC的平分線BE交AC于點E,交CD于點F;
(3)觀察線段CE與CF有何數(shù)量關系?并說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com