
【題目】如圖,已知點![]() 在
在![]() 的
的![]() 邊上,
邊上,![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,若添加條件________,則四邊形
,若添加條件________,則四邊形![]() 是矩形;若添加條件________,則四邊形
是矩形;若添加條件________,則四邊形![]() 是菱形;若添加條件________,則四邊形
是菱形;若添加條件________,則四邊形![]() 是正方形.
是正方形.

【答案】![]()
![]() 平分
平分![]()
![]() 且
且![]() 平分
平分![]()
【解析】
根據(jù)已知條件判定四邊形AEDF是平行四邊形,再根據(jù)矩形、菱形、正方形的判定方法添加適當?shù)臈l件即可解答.
∵DE∥AC,DF∥AB,
∴四邊形AEDF是平行四邊形;
①添加條件:![]() ,根據(jù)有一個角是直角的平行四邊形為矩形即可得四邊形
,根據(jù)有一個角是直角的平行四邊形為矩形即可得四邊形![]() 是矩形;
是矩形;
②添加條件:![]() 平分
平分![]() ,可得∠DAF=∠DAE,由DE∥AC,∠ADE=∠DAF,所以∠ADE =∠DAE,即可得AE=ED,根據(jù)一組鄰邊相等的平行四邊形為菱形即可得四邊形AEDF是菱形;
,可得∠DAF=∠DAE,由DE∥AC,∠ADE=∠DAF,所以∠ADE =∠DAE,即可得AE=ED,根據(jù)一組鄰邊相等的平行四邊形為菱形即可得四邊形AEDF是菱形;
③添加條件:![]() 且
且![]() 平分
平分![]() ,在①②的基礎上即可判定四邊形AEDF是正方形.
,在①②的基礎上即可判定四邊形AEDF是正方形.
故答案為: ∠BAC=90°;AD平分∠BAC;∠BAC=90°且AD平分∠BAC.


 智能訓練練測考系列答案
智能訓練練測考系列答案科目:初中數(shù)學 來源: 題型:
【題目】如圖,AD,AE分別是△ABC的角平分線和高線,∠B=45°,∠C=73°.
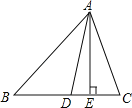
(1)求∠ADB的度數(shù);
(2)求∠DAE的度數(shù).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,已知![]() ,
,![]() 是一次函數(shù)
是一次函數(shù)![]() 的圖象和反比例函數(shù)
的圖象和反比例函數(shù)![]() 的圖象的兩個交點.
的圖象的兩個交點.
![]() 求直線
求直線![]() 與
與![]() 軸的交點
軸的交點![]() 的坐標及
的坐標及![]() 的面積;
的面積;
![]() 在
在![]() 軸上是否存在一點
軸上是否存在一點![]() ,使得
,使得![]() 的值最大?若存在,直接寫出點
的值最大?若存在,直接寫出點![]() 的坐標;若不存在,請說明理由;
的坐標;若不存在,請說明理由;
![]() 當點
當點![]() 在雙曲線上運動時,作以
在雙曲線上運動時,作以![]() 、
、![]() 為鄰邊的平行四邊形,求平行四邊形周長最小時點
為鄰邊的平行四邊形,求平行四邊形周長最小時點![]() 的坐標.
的坐標.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在⊙O中,將![]() 沿弦BC所在直線折疊,折疊后的弧與直徑AB相交于點D,連接CD.
沿弦BC所在直線折疊,折疊后的弧與直徑AB相交于點D,連接CD.
(1)若點D恰好與點O重合,則∠ABC= °;
(2)延長CD交⊙O于點M,連接BM.猜想∠ABC與∠ABM的數(shù)量關系,并說明理由.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】五一期間,小明一家一起去旅游,如圖是小明設計的某旅游景點的圖紙(網(wǎng)格是由相同的小正方形組成的,且小正方形的邊長代表實際長度100m),在該圖紙上可看到兩個標志性景點A,B.若建立適當?shù)钠矫嬷苯亲鴺讼担瑒t點A(-3,1),B(-3,-3),第三個景點C(3,2)的位置已破損.
(1)請在圖中標出景點C的位置;
(2)小明想從景點B開始游玩,途經(jīng)景點A,最后到達景點C,求小明一家最短的行走路程(參考數(shù)據(jù):![]() ≈6,結(jié)果保留整數(shù)).
≈6,結(jié)果保留整數(shù)).

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】對于一個關于![]() 的代數(shù)式
的代數(shù)式![]() ,若存在一個系數(shù)為正數(shù)關于
,若存在一個系數(shù)為正數(shù)關于![]() 的單項式
的單項式![]() ,使
,使![]() 的結(jié)果是所有系數(shù)均為整數(shù)的整式,則稱單項式
的結(jié)果是所有系數(shù)均為整數(shù)的整式,則稱單項式![]() 為代數(shù)式
為代數(shù)式![]() 的“整系單項式” ,例如:
的“整系單項式” ,例如:
當![]() 時,由于
時,由于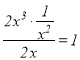 ,故
,故![]() 是
是![]() 的整系單項式;
的整系單項式;
當![]() 時,由于
時,由于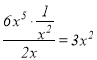 ,故
,故![]() 是
是![]() 的整系單項式;
的整系單項式;
當![]() 時,由于
時,由于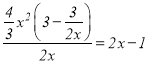 ,故
,故![]() 是
是![]() 的整系單項式;
的整系單項式;
當![]() 時,由于
時,由于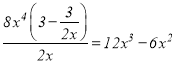 ,故
,故![]() 是
是![]() 的整系單項式;
的整系單項式;
顯然,當代數(shù)式![]() 存在整系單項式
存在整系單項式![]() 時,
時,![]() 有無數(shù)個,現(xiàn)把次數(shù)最低,系數(shù)最小的整系單項式
有無數(shù)個,現(xiàn)把次數(shù)最低,系數(shù)最小的整系單項式![]() 記為
記為![]() ,例如:
,例如:![]() .
.
閱讀以上材料并解決下列問題:
⑴.判斷:當![]() 時,
時,![]()
![]() 的整系單項式(填“是”或“不是”);
的整系單項式(填“是”或“不是”);
⑵.當![]() 時,
時,![]() = ;
= ;
⑶.解方程: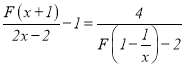 .
.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
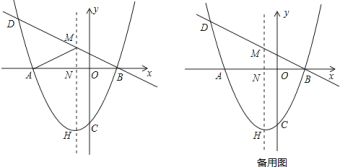
【題目】如圖,拋物線![]() 交
交![]() 軸于
軸于![]() 、
、![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() ,頂點為
,頂點為![]() ,其對稱軸交
,其對稱軸交![]() 軸于點
軸于點![]() .直線
.直線![]() 經(jīng)過
經(jīng)過![]() 、
、![]() 兩點,交拋物線的對稱軸于點
兩點,交拋物線的對稱軸于點![]() ,其中點
,其中點![]() 的橫坐標為
的橫坐標為![]() .
.
(1)求拋物線的表達式;
(2)連接![]() ,求
,求![]() 的周長;
的周長;
(3)若![]() 是拋物線位于直線
是拋物線位于直線![]() 的下方且在其對稱軸左側(cè)上的一點,當四邊形
的下方且在其對稱軸左側(cè)上的一點,當四邊形![]() 的面積最大時,求點
的面積最大時,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某校為了創(chuàng)建書香校園,去年又購進了一批圖書.經(jīng)了解,科普書的單價比文學書的單價多4元,用1200元購進的科普書與用800元購進的文學書本數(shù)相等.
(1)求去年購進的文學羽和科普書的單價各是多少元?
(2)若今年文學書和科普書的單價和去年相比保持不變,該校打算用1000元再購進一批文學書和科普書,問購進文學書55本后至多還能購進多少本科普書?
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com