
【題目】綜合與探究
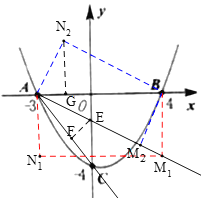
如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點(diǎn),與
兩點(diǎn),與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() .
.
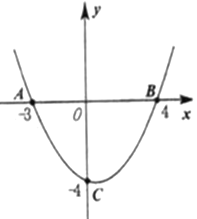
(1)求拋物線解析式:
(2)拋物線對(duì)稱軸上存在一點(diǎn)![]() ,連接
,連接![]() 、
、![]() ,當(dāng)
,當(dāng)![]() 值最大時(shí),求點(diǎn)H坐標(biāo):
值最大時(shí),求點(diǎn)H坐標(biāo):
(3)若拋物線上存在一點(diǎn)![]() ,
,![]() ,當(dāng)
,當(dāng)![]() 時(shí),求點(diǎn)
時(shí),求點(diǎn)![]() 坐標(biāo):
坐標(biāo):
(4)若點(diǎn)M是![]() 平分線上的一點(diǎn),點(diǎn)
平分線上的一點(diǎn),點(diǎn)![]() 是平面內(nèi)一點(diǎn),若以
是平面內(nèi)一點(diǎn),若以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點(diǎn)的四邊形是矩形,請(qǐng)直接寫出點(diǎn)
為頂點(diǎn)的四邊形是矩形,請(qǐng)直接寫出點(diǎn)![]() 坐標(biāo).
坐標(biāo).
【答案】(1)![]() ;(2)點(diǎn)
;(2)點(diǎn)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() ,
,![]()
【解析】
(1)把A、B兩點(diǎn)坐標(biāo)代入拋物線解析式,解方程組求出a、b的值即可得答案;(2)連接AC,延長(zhǎng)AC交拋物線對(duì)稱軸與H,由A、C兩點(diǎn)坐標(biāo)可得直線AC的解析式,根據(jù)拋物線解析式可得對(duì)稱軸方程,根據(jù)A、C、H三點(diǎn)在一條直線時(shí),![]() 的值最大,即可得答案;(3)由C點(diǎn)坐標(biāo)可得△ABC和△ABP的高為4,可得P點(diǎn)縱坐標(biāo)n=±4,把n=±4代入拋物線解析式求出m的值,根據(jù)mn>0即可得P點(diǎn)坐標(biāo);(4)設(shè)∠BAC的角平分線與y軸交于E點(diǎn),過(guò)點(diǎn)E作EF⊥AC,根據(jù)角平分線的性質(zhì)可證明△AFE≌△AOE,可得出AF的長(zhǎng),利用勾股定理可求出OE的長(zhǎng),可得E點(diǎn)坐標(biāo),進(jìn)而利用待定系數(shù)法可求出直線AE的解析式,分兩種情況:①當(dāng)∠ABM1=90°時(shí),M1N1=AB,AN1=BM,M1B⊥x軸,可得點(diǎn)M1的橫坐標(biāo),代入AE的解析式可得點(diǎn)M1的縱坐標(biāo),即可得出BM的長(zhǎng),進(jìn)而可得N1點(diǎn)坐標(biāo);②當(dāng)∠AM2B=90°時(shí),可知∠N2BA=∠BAE,過(guò)N2作N2G⊥x軸,根據(jù)點(diǎn)E坐標(biāo)可得∠BAE的正弦值和余弦值,即可求出BN2的長(zhǎng),利用∠N2BA的正弦和余弦可求出N2G和BG的長(zhǎng),進(jìn)而可得OG的長(zhǎng),即可得N2坐標(biāo);綜上即可得答案.
的值最大,即可得答案;(3)由C點(diǎn)坐標(biāo)可得△ABC和△ABP的高為4,可得P點(diǎn)縱坐標(biāo)n=±4,把n=±4代入拋物線解析式求出m的值,根據(jù)mn>0即可得P點(diǎn)坐標(biāo);(4)設(shè)∠BAC的角平分線與y軸交于E點(diǎn),過(guò)點(diǎn)E作EF⊥AC,根據(jù)角平分線的性質(zhì)可證明△AFE≌△AOE,可得出AF的長(zhǎng),利用勾股定理可求出OE的長(zhǎng),可得E點(diǎn)坐標(biāo),進(jìn)而利用待定系數(shù)法可求出直線AE的解析式,分兩種情況:①當(dāng)∠ABM1=90°時(shí),M1N1=AB,AN1=BM,M1B⊥x軸,可得點(diǎn)M1的橫坐標(biāo),代入AE的解析式可得點(diǎn)M1的縱坐標(biāo),即可得出BM的長(zhǎng),進(jìn)而可得N1點(diǎn)坐標(biāo);②當(dāng)∠AM2B=90°時(shí),可知∠N2BA=∠BAE,過(guò)N2作N2G⊥x軸,根據(jù)點(diǎn)E坐標(biāo)可得∠BAE的正弦值和余弦值,即可求出BN2的長(zhǎng),利用∠N2BA的正弦和余弦可求出N2G和BG的長(zhǎng),進(jìn)而可得OG的長(zhǎng),即可得N2坐標(biāo);綜上即可得答案.
(1)∵A(-3,0),B(4,0),點(diǎn)A、B在拋物線上,
∴![]()
解得: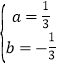 ,
,
∴拋物線的解析式為:y=![]() x2-
x2-![]() x-4.
x-4.
(2)連接AC,延長(zhǎng)AC交拋物線對(duì)稱軸與H,
∵拋物線解析式為y=![]() x2-
x2-![]() x-4,與
x-4,與![]() 軸交于點(diǎn)C
軸交于點(diǎn)C
∴C(0,-4),對(duì)稱軸為直線x=-![]() =
=![]() ,
,
∵![]() ≤AC,
≤AC,
∴A、C、H在一條直線上時(shí)![]() 取最小值,
取最小值,
設(shè)直線AC的解析式為y=kx+b,
∴![]() ,
,
解得: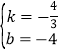 ,
,
∴直線AC的解析式為y=![]() x-4,
x-4,
當(dāng)x=![]() 時(shí),y=
時(shí),y=![]() ,
,
∴H點(diǎn)坐標(biāo)為(![]() ,
,![]() ).
).
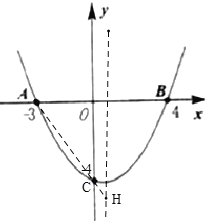
(3)∵S△ABC=S△ABP,
∴![]() AB
AB![]() OC=
OC=![]() AB
AB![]()
![]() ,
,
∴![]() =4,
=4,
當(dāng)n=4時(shí),4=![]() m2-
m2-![]() m-4,
m-4,
解得m=![]() ,
,
∵mn>0,
∴m=![]() ,
,
∴P點(diǎn)坐標(biāo)為(![]() ,4)
,4)
當(dāng)n=-4時(shí),-4=![]() m2-
m2-![]() m-4,
m-4,
解得:m=1或m=0,
∵mn>0,
∴m=1或m=0均不符合題意,
綜上:P點(diǎn)坐標(biāo)為(![]() ,4).
,4).
(4)設(shè)∠BAC的角平分線交y軸于E,過(guò)E作EF⊥AC于F,
∵A(-3,0),B(4,0),C(0,-4),
∴AB=7,AC=5,OA=3,OC=4,
∵AE為∠BAC的角平分線,
∴OE=EF,
又∵AE=AE,
△AOE≌△FAE,
∴AF=OA=3,
∴FC=5-3=2,
∴EF2+FC2=CE2,即OE2+22=(4-OE)2,
解得:OE=![]() ,
,
∵點(diǎn)E在y軸負(fù)半軸,
∴E點(diǎn)坐標(biāo)為(0,-![]() ),
),
設(shè)直線AE的解析式為y=kx+b,
∴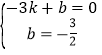
解得: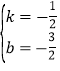
∴直線AE的解析式為y=![]() ,
,
①當(dāng)∠ABM1=90°時(shí),
∵ANMB是矩形,
∴M1N1=AB=7,AN1=BM,M1B⊥x軸,AN1⊥x軸,
∴x=4時(shí),y=![]() ,
,
∴點(diǎn)N1坐標(biāo)為(-3,![]() ).
).
②當(dāng)∠AM2B=90°時(shí),過(guò)N2作N2G⊥x軸,
∵AM2BN2是矩形,
∴∠N2BA=∠BAE,
∵OA=3,OE=![]() ,
,
∴AE=![]() ,
,
∴sin∠BAE=![]() =
=![]() ,cos∠BAE=
,cos∠BAE=![]() =
=![]() ,
,
∴sin∠N2BA =![]() ,cos∠N2BA=
,cos∠N2BA=![]()
∴BN2=AB![]() cos∠N2BA=
cos∠N2BA=![]() ,
,
∴N2G=BN2![]() sin∠N2BA=
sin∠N2BA=![]() ,BG=BN2
,BG=BN2![]() cos∠N2BA=
cos∠N2BA=![]() ,
,
∴OB-BG=-![]() ,
,
∴點(diǎn)N2坐標(biāo)為(-![]() ,
,![]() ).
).
綜上所述:點(diǎn)N的坐標(biāo)為N1(-3,![]() ),N2(-
),N2(-![]() ,
,![]() ).
).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】跳繩是大家喜聞樂(lè)見(jiàn)的一項(xiàng)體育運(yùn)動(dòng),集體跳繩時(shí),需要兩人同頻甩動(dòng)繩子,當(dāng)繩子甩到最高處時(shí),其形狀可近似看作拋物線,下圖是小明和小亮甩繩子到最高處時(shí)的示意圖,兩人拿繩子的手之間的距離為4![]() ,離地面的高度為1
,離地面的高度為1![]() ,以小明的手所在位置為原點(diǎn)建立平面直角坐標(biāo)系.
,以小明的手所在位置為原點(diǎn)建立平面直角坐標(biāo)系.
(1)當(dāng)身高為15![]() 的小紅站在繩子的正下方,且距小明拿繩子手的右側(cè)1
的小紅站在繩子的正下方,且距小明拿繩子手的右側(cè)1![]() 處時(shí),繩子剛好通過(guò)小紅的頭頂,求繩子所對(duì)應(yīng)的拋物線的表達(dá)式;
處時(shí),繩子剛好通過(guò)小紅的頭頂,求繩子所對(duì)應(yīng)的拋物線的表達(dá)式;
(2)若身高為![]() 的小麗也站在繩子的正下方.
的小麗也站在繩子的正下方.
①當(dāng)小麗在距小亮拿繩子手的左側(cè)1.5![]() 處時(shí),繩子能碰到小麗的頭嗎?請(qǐng)說(shuō)明理由;
處時(shí),繩子能碰到小麗的頭嗎?請(qǐng)說(shuō)明理由;
②設(shè)小麗與小亮拿繩子手之間的水平距離為![]() ,為保證繩子不碰到小麗的頭頂,求
,為保證繩子不碰到小麗的頭頂,求![]() 的取值范圍.(參考數(shù)據(jù):
的取值范圍.(參考數(shù)據(jù): ![]() 取3.16)
取3.16)

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 在
在![]() 邊上,把
邊上,把![]() 沿
沿![]() 折疊后,使得點(diǎn)
折疊后,使得點(diǎn)![]() 落在點(diǎn)
落在點(diǎn)![]() 處,連接
處,連接![]() ,若
,若![]() ,則
,則![]() ______.
______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
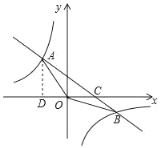
【題目】如圖,在平面直角坐標(biāo)系xOy中,一次函數(shù)y=kx+b(k≠0)的圖象與反比例函數(shù)y=![]() (n≠0)的圖象交于第二、四象限內(nèi)的A、B兩點(diǎn)與x軸交于點(diǎn)C,點(diǎn)B坐標(biāo)為(m,﹣1),AD⊥x軸,且AD=3,tan∠AOD=
(n≠0)的圖象交于第二、四象限內(nèi)的A、B兩點(diǎn)與x軸交于點(diǎn)C,點(diǎn)B坐標(biāo)為(m,﹣1),AD⊥x軸,且AD=3,tan∠AOD=![]()
(1)求該反比例函數(shù)和一次函數(shù)的解析式;
(2)連接OB,求S△AOC﹣S△BOC的值;
(3)點(diǎn)E是x軸上一點(diǎn),且△AOE是等腰三角形請(qǐng)直接寫出滿足條件的E點(diǎn)的個(gè)數(shù)(寫出個(gè)數(shù)即可,不必求出E點(diǎn)坐標(biāo)).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
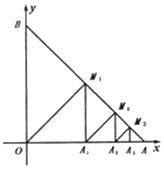
【題目】在平面直角坐標(biāo)系中,點(diǎn)![]() 在
在![]() 軸正半軸上,點(diǎn)
軸正半軸上,點(diǎn)![]() 在
在![]() 軸正半軸上,
軸正半軸上,![]() 為坐標(biāo)原點(diǎn),
為坐標(biāo)原點(diǎn),![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() :過(guò)點(diǎn)
:過(guò)點(diǎn)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() :過(guò)點(diǎn)
:過(guò)點(diǎn)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() :過(guò)點(diǎn)
:過(guò)點(diǎn)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() …以此類推,點(diǎn)
…以此類推,點(diǎn)![]() 的坐標(biāo)為__________.
的坐標(biāo)為__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
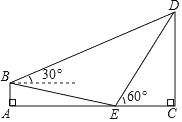
【題目】如圖,斜坡BE,坡頂B到水平地面的距離AB為3米,坡底AE為18米,在B處,E處分別測(cè)得CD頂部點(diǎn)D的仰角為30°,60°,求CD的高度.(結(jié)果保留根號(hào))
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
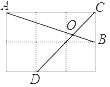
【題目】如圖,在邊長(zhǎng)為1的小正方形網(wǎng)格中,點(diǎn)A,B,C,D都在這些小正方形上,AB與CD相交于點(diǎn)O,則tan∠AOD等于( )
A. ![]() B. 2C. 1D.
B. 2C. 1D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列說(shuō)法:①平方等于其本身的數(shù)有0,±1;②32xy3是4次單項(xiàng)式;③將方程![]() 中的分母化為整數(shù),得
中的分母化為整數(shù),得![]() =12;④平面內(nèi)有4個(gè)點(diǎn),過(guò)每?jī)牲c(diǎn)畫直線,可畫6條、4條或1條.其中正確的有( )
=12;④平面內(nèi)有4個(gè)點(diǎn),過(guò)每?jī)牲c(diǎn)畫直線,可畫6條、4條或1條.其中正確的有( )
A. 1個(gè)B. 2個(gè)C. 3個(gè)D. 4個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
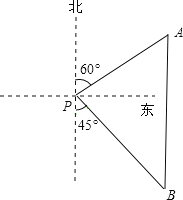
【題目】如圖,一艘漁船位于海洋觀測(cè)站P的北偏東60°方向,漁船在A處與海洋觀測(cè)站P的距離為60海里,它沿正南方向航行一段時(shí)間后,到達(dá)位于海洋觀測(cè)站P的南偏東45°方向上的B處.求此時(shí)漁船所在的B處與海洋觀測(cè)站P的距離(結(jié)果保留根號(hào)).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com