
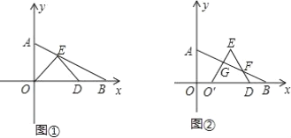
【題目】如圖,在Rt△AOB中,∠ABO=30°,BO=4,分別以OA、OB邊所在的直線建立平面直角坐標系,D點為x軸正半軸上的一點,以OD為一邊在第一象限內作等邊△ODE.
(1)如圖①當E點恰好落在線段AB上時,求E點坐標;
(2)若點D從原點出發沿x軸正方向移動,設點D到原點的距離為x,△ODE與△AOB重疊部分的面積為y,當E點到達△AOB的外面,且點D在點B左側時,寫出y與x的函數關系式,并寫出自變量x的取值范圍;
(3)在(1)問的條件下,將△ODE在線段OB上向右平移如圖②,圖中是否存在一條與線段OO′始終相等的線段?如果存在,請直接指出這條線段;如果不存在,請說明理由.
【答案】(1)E(1,![]() );(2)y=﹣
);(2)y=﹣![]() x2+2
x2+2![]() x﹣2
x﹣2![]() (2<x<4);(3)存在線段EF=OO';理由見解析
(2<x<4);(3)存在線段EF=OO';理由見解析
【解析】
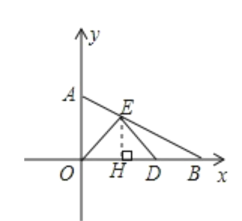
(1)根據題意,作EH⊥OB于點H,由BO=4,求得OE,然后求出OH,EH,從而得出點E的坐標;
(2)根據題意,當E點到達△AOB的外面,且點D在點B左側時,2<x<4即可;
(3)假設存在,由OO′=4﹣2﹣DB,而DF=DB,從而得到EF=OO'.
解:(1)作EH⊥OB于點H,
∵△OED是等邊三角形,
∴∠EOD=60°.
又∵∠ABO=30°,
∴∠OEB=90°.
∵BO=4,
∴OE=![]() OB=2.
OB=2.
∵△OEH是直角三角形,且∠OEH=30°,
∴OH=![]() OE=1,EH=
OE=1,EH=![]() ,
,
∵點E在第一象限內,
∴E(1,![]() ),
),
故答案為:E(1,![]() );
);
(2)當2<x<4,符合題意,如圖,
由(1)知∠OEB=90°,∠E′=60°,
所求重疊部分四邊形OD′NE的面積為:
S△OD′E′﹣S△E′EN=![]() OD×EH﹣
OD×EH﹣![]() E′E×EN=
E′E×EN=![]() x2﹣
x2﹣![]() ×
×![]() (x﹣2)=﹣
(x﹣2)=﹣![]() x2+2
x2+2![]() x﹣2
x﹣2![]()
∴y=﹣![]() x2+2
x2+2![]() x﹣2
x﹣2![]() (2<x<4),
(2<x<4),
故答案為:y=﹣![]() x2+2
x2+2![]() x﹣2
x﹣2![]() (2<x<4);
(2<x<4);
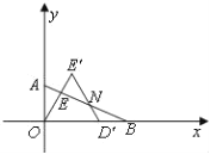
(3)存在線段EF=OO'.
∵∠ABO=30°,∠EDO=60°,
∴∠ABO=∠DFB=30°,
∴DF=DB,
∴OO′=4﹣2﹣DB=2﹣DB=2﹣DF=ED﹣DF=EF,
故答案為:存在線段EF=OO'.


科目:初中數學 來源: 題型:
【題目】拋物線![]() 的部分圖象如圖所示,與x軸的一個交點坐標為
的部分圖象如圖所示,與x軸的一個交點坐標為![]() ,拋物線的對稱軸是
,拋物線的對稱軸是![]() 下列結論中:
下列結論中:
![]() ;
;![]() ;
;![]() 方程
方程![]() 有兩個不相等的實數根;
有兩個不相等的實數根;![]() 拋物線與x軸的另一個交點坐標為
拋物線與x軸的另一個交點坐標為![]() ;
;![]() 若點
若點![]() 在該拋物線上,則
在該拋物線上,則![]() .
.
其中正確的有![]()
![]()

A. 5個 B. 4個 C. 3個 D. 2個
查看答案和解析>>
科目:初中數學 來源: 題型:
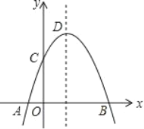
【題目】如圖,拋物線y=﹣x2+2x+m+1交x軸于點A(a,0)和B(b,0),交y軸于點C,拋物線的頂點為D,下列四個命題:
①當x>0時,y>0;
②若a=﹣1,則b=3;
③拋物線上有兩點P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,則y1>y2;
④點C關于拋物線對稱軸的對稱點為E,點G,F分別在x軸和y軸上,當m=2時,四邊形EDFG周長的最小值為6![]() .
.
其中真命題的序號是____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形EFGH的頂點E,G分別在菱形ABCD的邊AD ,BC上,頂點F,H在菱形ABCD的對角線BD上,若AB=6,∠A=120°,且DE=2,則FH=_______.
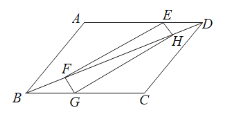
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知矩形![]() 的兩邊OA,OC分別落在
的兩邊OA,OC分別落在![]() 軸,
軸,![]() 軸的正半軸上,
軸的正半軸上,![]() 的坐標為
的坐標為![]() ,反比例函數
,反比例函數![]() 的圖象經過
的圖象經過![]() 的中點E,且與BC邊相交于點D.
的中點E,且與BC邊相交于點D.
(1)①求反比例函數的解析式及點D的坐標;
②直接寫出![]() 的面積為________.
的面積為________.
(2)若P是OA上的動點,當![]() 值為最小時,求直線
值為最小時,求直線![]() 的解析式.
的解析式.
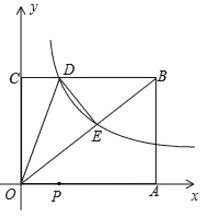
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,一次函數![]() 的圖像與反比例函數
的圖像與反比例函數![]() 的圖像交于
的圖像交于![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() .
.
(1)求![]() 的值;
的值;
(2)請直接寫出不等式![]() 的解集;
的解集;
(3)將![]() 軸下方的圖像沿
軸下方的圖像沿![]() 軸翻折,點
軸翻折,點![]() 落在點
落在點![]() 處,連接
處,連接![]() ,求
,求![]() 的面積.
的面積.
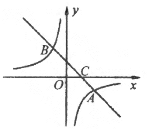
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據北京市統計局發布的統計數據顯示,北京市近五年國民生產總值數據如圖1所示,2017年國民生產總值中第一產業、第二產業、第三產業所占比例如圖2所示,根據以上信息,下列判斷錯誤的是( )
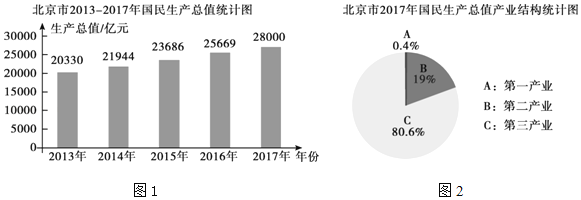
A.2013年至2017年北京市國民生產總值逐年增加
B.2017年第二產業生產總值為5 320億元
C.2017年比2016年的國民生產總值增加了10%
D.若從2018年開始,每一年的國民生產總值比前一年均增長10%,到2019年的國民生產總值將達到33 880億元
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com