
【題目】我們知道![]() ,于是我們說:“
,于是我們說:“![]() 的整數部分為
的整數部分為![]() ,小數部分則可記為
,小數部分則可記為![]() ”.則:
”.則:
(1)![]() 的整數部分為________,小數部分則可記為________;
的整數部分為________,小數部分則可記為________;
(2)已知![]() 的小數部分為
的小數部分為![]() ,
,![]() 的小數部分為
的小數部分為![]() ,那么
,那么![]() 的值是________;
的值是________;
(3)已知![]() 是
是![]() 的整數部分,
的整數部分,![]() 是
是![]() 的小數部分,求
的小數部分,求![]() 的平方根.
的平方根.
【答案】(1)-1,![]() -2;(2)1;(3)±3.
-2;(2)1;(3)±3.
【解析】
(1)先估算出![]() -3的取值范圍,進而可得出結論;
-3的取值范圍,進而可得出結論;
(2)估算出3+![]() 與7-
與7-![]() 的取值范圍,故可得出a與b的值,代入代數式進行計算即可;
的取值范圍,故可得出a與b的值,代入代數式進行計算即可;
(3)先估算出![]() 的取值范圍,故可得出x、y的值,代入代數式進行計算即可.
的取值范圍,故可得出x、y的值,代入代數式進行計算即可.
(1)∵1<2<4,
∴1<![]() <3,
<3,
∴1-3<![]() -3<0,即-2<
-3<0,即-2<![]() -3<0,
-3<0,
∴![]() -3的整數部分是-1,小數部分是
-3的整數部分是-1,小數部分是![]() -2.
-2.
故答案為:-1,![]() -2;
-2;
(2)∵25<31<36,
∵5<![]() <6,
<6,
∴8<3+![]() <9,
<9,
∴3+![]() 的小數部分是
的小數部分是![]() -5,即a=
-5,即a=![]() -5;
-5;
同理,∵25<31<36,
∵-6<-![]() <-5,
<-5,
∴1<7-![]() <2
<2
∴7-![]() 的小數部分為7-
的小數部分為7-![]() -1=6-
-1=6-![]() ,即b=6-
,即b=6-![]() ,
,
∴a+b=![]() -5+6-
-5+6-![]() =1.
=1.
故答案為:1;
(3)∵9<10<16,
∴3<![]() <4,
<4,
∴![]() 的整數部分是3,小數部分是
的整數部分是3,小數部分是![]() -3,即a=3,y=
-3,即a=3,y=![]() -3,
-3,
∴(y![]() )x1=(
)x1=(![]() -3-
-3-![]() )3-1=(-3)2=9,
)3-1=(-3)2=9,
∵±![]() =±3,
=±3,
∴(y![]() )x1的平方根是±3.
)x1的平方根是±3.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知數軸上點A表示的數為-7,點B表示的數為5,點C到點A,點B的距離相等,動點P從點A出發,以每秒2個單位長度的速度沿數軸向右勻速運動,設運動的時間為![]() (
(![]() >0)秒
>0)秒
(1)點C表示的數是_________.
(2)求當![]() 等于多少秒時,點P到達點B處.
等于多少秒時,點P到達點B處.
(3)點P表示的數是_________(用含有![]() 的代數式表示).
的代數式表示).
(4)求當t等于多少秒時,PC之間的距離為2個單位長度(只列式,不計算).
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,E、F分別是邊AB、CD上的點,AE=CF,連接EF,BF,EF與對角線AC交于O點,且BE=BF,∠BEF=2∠BAC。

(1)求證:OE=OF;
(2)若BC=![]() ,求AB的長。
,求AB的長。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列單項式:![]() ,
,![]() ,
,![]() ,
,![]() ,…
,…![]() ,
,![]() ,…寫出第
,…寫出第![]() 個單項式,為了解這個問題,特提供下面的解題思路.
個單項式,為了解這個問題,特提供下面的解題思路.
![]() 這組單項式的系數的符號,絕對值規律是什么?
這組單項式的系數的符號,絕對值規律是什么?
![]() 這組單項式的次數的規律是什么?
這組單項式的次數的規律是什么?
![]() 根據上面的歸納,你可以猜想出第
根據上面的歸納,你可以猜想出第![]() 個單項式是什么?
個單項式是什么?
![]() 請你根據猜想,請寫出第
請你根據猜想,請寫出第![]() 個,第
個,第![]() 個單項式.
個單項式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.

(1)求DE的長;
(2)求△ADB的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,二次函數y=ax2+2ax﹣3a(a≠0)圖象的頂點為H,與x軸交于A、B兩點(B在A點右側),點H、B關于直線l: ![]() 對稱.
對稱. 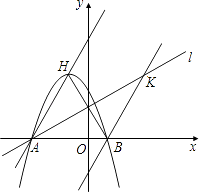
(1)求A、B兩點坐標,并證明點A在直線l上;
(2)求二次函數解析式; 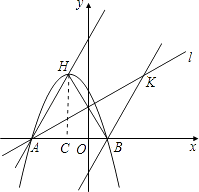
(3)過點B作直線BK∥AH交直線l于K點,M、N分別為直線AH和直線l上的兩個動點,連接HN、NM、MK,求HN+NM+MK和的最小值. 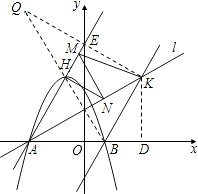
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明去文具用品商店給同學買某品牌水性筆,已知甲、乙兩商店都有該品牌的水性筆且標價都是2元/支,但甲、乙兩商店的優惠條件卻不同.
甲商店:若購買不超過10支,則按標價付款;若一次購10支以上,則超過10支的部分按標價的60%付款. 乙商店:按標價的80%付款.
在水性筆的質量等因素相同的條件下.
(1)設小明要購買的該品牌筆數是x(x>10)支,請用含x的式子分別表示在甲、乙兩個商店購買該品牌筆買水性筆的費用.
(2)若小明要購買該品牌筆30支,你認為在甲、乙兩商店中,到哪個商店購買比較省錢?說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com