
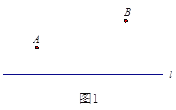
【題目】問題:如圖1,點(diǎn)![]() ,
,![]() 在直線
在直線![]() 的同側(cè),在直線
的同側(cè),在直線![]() 上找一點(diǎn)
上找一點(diǎn)![]() ,使得
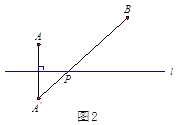
,使得![]() 的值最小.小明的思路是:如圖2,作點(diǎn)
的值最小.小明的思路是:如圖2,作點(diǎn)![]() 關(guān)于直線
關(guān)于直線![]() 的對稱點(diǎn)
的對稱點(diǎn)![]() ,連接
,連接![]() ,則
,則![]() 與直線
與直線![]() 的交點(diǎn)
的交點(diǎn)![]() 即為所求.
即為所求.
請你參考小明同學(xué)的思路,探究并解決下列問題:
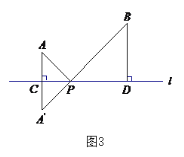
(1)如圖3,在圖2的基礎(chǔ)上,設(shè)![]() 與直線
與直線![]() 的交點(diǎn)為
的交點(diǎn)為![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() ,垂足為
,垂足為![]() . 若
. 若![]() ,
,![]() ,
,![]() ,寫出
,寫出![]() 的值為____________;
的值為____________;
(2)將(1)中的條件“![]() ”去掉,換成“
”去掉,換成“![]() ”,其它條件不變,寫出此時
”,其它條件不變,寫出此時![]() 的值 ___________;
的值 ___________;
(3)求![]() +
+![]() 的最小值.
的最小值.
【答案】 3![]() 5;
5;![]()
【解析】(1)、由勾股定理和相似三角形的性質(zhì),求得AP,BP的值即可;(2)、由勾股定理和相似三角形的性質(zhì),建立方程求解;(3)、結(jié)合圖形,由(1)(2)直接寫出即可.
(1)、如圖2,∵AA′⊥l,AC=1,PC=1,
∴PA=![]() ,∴PA′=PA=
,∴PA′=PA=![]() ,∵AA′∥BD,∴∠A′=∠B,∵∠A′PC=∠BPD,
,∵AA′∥BD,∴∠A′=∠B,∵∠A′PC=∠BPD,
∴△A′PC∽△BPD,∴![]() ,∴
,∴![]() ,∴PB=2
,∴PB=2![]() , ∴AP+PB=
, ∴AP+PB=![]() +2
+2![]() =3
=3![]() ;
;
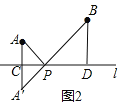
(2)、作AE∥l,交BD的延長線于E,如圖3,
則四邊形A′EDC是矩形,∴AE=DC=PC+PD=3,DE=A′C=AC,∵BD=4-AC,
∴BD+AC=BD+DE=4,即BE=4,在Rt△A′BE中,A′B=![]() =5,∴AP+BP=5,
=5,∴AP+BP=5,
(3)、如圖3,設(shè)AC=2m-3,PC=1,則PA=![]() ;設(shè)BD=8-2m,PD=2,
;設(shè)BD=8-2m,PD=2,
則PB=![]() ,∵DE=AC=2m-3,∴BE=BD+DE=5,A′E=CD=PC+PD=3
,∵DE=AC=2m-3,∴BE=BD+DE=5,A′E=CD=PC+PD=3
∴PA+PB=A′B=![]() .
.



 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
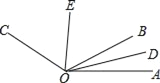
【題目】如圖,OD是∠AOB的平分線,OE是∠BOC的平分線.
(1)若∠BOC=50°,∠BOA=80°,求∠DOE的度數(shù);
(2)若∠AOC=150°,求∠DOE的度數(shù);
(3)你發(fā)現(xiàn)∠DOE與∠AOC有什么等量關(guān)系?給出結(jié)論并說明.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,P是矩形ABCD的AD邊上一個動點(diǎn),矩形的兩條邊AB、BC長分別是6和8,則點(diǎn)P到矩形的兩條對角線距離之和PE+PF是( )
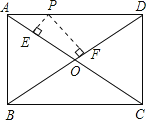
A. 4.8 B. 5 C. 6 D. 7.2
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】將一條長為20cm的鐵絲剪成兩段,并以每一段鐵絲的長度為周長做成一個正方形.
(1)要使這兩個正方形的面積之和等于17cm2,那么這段鐵絲剪成兩段后的長度分別是多少?
(2)兩個正方形的面積之和可能等于12cm2嗎? 若能,求出兩段鐵絲的長度;若不能,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】閱讀下列材料:
小明遇到一個問題:AD是△ABC的中線, 點(diǎn)M為BC邊上任意一點(diǎn)(不與點(diǎn)D重合),過點(diǎn)M作一直線,使其等分△ABC的面積.
他的做法是:如圖1,連結(jié)AM,過點(diǎn)D作DN//AM交AC于點(diǎn)N,作直線MN,直線MN即為所求直線.
請你參考小明的做法,解決下列問題:
(1)如圖2, AE等分四邊形ABCD的面積,M為CD邊上一點(diǎn),過M作一直線MN,使其等分四邊形ABCD的面積(要求:在圖2中畫出直線MN,并保留作圖痕跡);
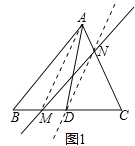
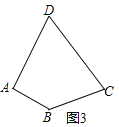
(2)如圖3,求作過點(diǎn)A的直線AE,使其等分四邊形ABCD的面積(要求:在圖3中畫出直線AE,并保留作圖痕跡).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
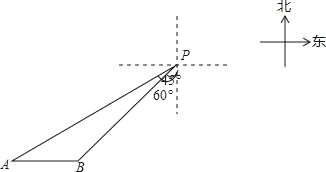
【題目】一艘輪船位于燈塔P南偏西60°方向的A處,它向東航行20海里到達(dá)燈塔P南偏西45°方向上的B處,若輪船繼續(xù)沿正東方向航行,求輪船航行途中與燈塔P的最短距離.(結(jié)果保留根號)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知代數(shù)式A=x2+3xy+x-![]() ,B=2x2-xy+4y-1
,B=2x2-xy+4y-1
(1)當(dāng)x=y=-2時,求2A-B的值;
(2)若2A-B的值與y的取值無關(guān),求x的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
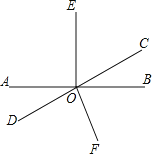
【題目】如圖,已知直線AB與直線CD相交于點(diǎn)O,∠BOE=90°,F(xiàn)O平分∠BOD,∠BOC:∠AOC=1:3.
(1)求∠DOE、∠COF的度數(shù).
(2)若射線OF、OE同時繞O點(diǎn)分別以2°/s、4°/s的速度,順時針勻速旋轉(zhuǎn),當(dāng)射線OE、OF的夾角為90°時,兩射線同時停止旋轉(zhuǎn).設(shè)旋轉(zhuǎn)時間為t,試求t值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,平行四邊形ABCD中,E,F(xiàn)是對角線BD上的兩點(diǎn),如果添加一個條件,使△ABE ≌ △CDF,則添加的條件不能為( )
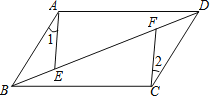
A. BE=DF B. BF=DE C. ∠1=∠2 D. AE=CF
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com