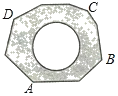
【題目】如圖，地面上有一個不規則的封閉圖形ABCD，為求得它的面積，小明在此封閉圖形內畫出一個半徑為2米的圓后，在附近閉上眼睛向封閉圖形內擲小石子（可把小石子近似地看成點），記錄如下：
擲小石子落在不規則圖形內的總次數 | 50 | 150 | 300 | … |
小石子落在圓內（含圓上）的次數m | 20 | 59 | 123 | … |
小石子落在圓外的陰影部分（含外緣）的次數n | 29 | 91 | 176 | … |
（1）當投擲的次數很大時，則m：n的值越來越接近 （結果精確到0.1）
（2）若以小石子所落的有效區域為總數（即m+n），則隨著投擲次數的增大，小石子落在圓內（含圓上）的頻率值穩定在 附近（結果精確到0.1）；
（3）請你利用（2）中所得頻率的值，估計整個封閉圖形ABCD的面積是多少平方米？（結果保留π）
【答案】（1）0.7；（2）0.4；（3）10π.
【解析】
（1）根據提供的m和n的值，計算m：n后即可確定二者的比值逐漸接近的值；
（2）大量試驗時，頻率可估計概率；
（3）利用概率，求出圓的面積比上總面積的值，計算出陰影部分面積．
解：（1）20÷29≈0.69；
59÷91≈0.65；
123÷176≈0.70，
…
當投擲的次數很大時，則m：n的值越來越接近0.7；
（2）20÷50=0.4；
59÷150≈0.39；
123÷300≈0.41
∴隨著投擲次數的增大，小石子落在圓內（含圓上）的頻率值穩定在0.4，
（3）設封閉圖形ABCD的面積為a，根據題意得：
，
解得：a=10π，
∴整個封閉圖形ABCD的面積為10π平方米.
科目：初中數學 來源： 題型：
【題目】如圖，在平行四邊形ABCD中，點M在BC邊上，且BM＝
BC，AM與BD相交于點N，那么S△BMN：S平行四邊形ABCD為（ ）
A.1：3B.1：9C.1：12D.1：24
查看答案和解析>>
科目：初中數學 來源： 題型：
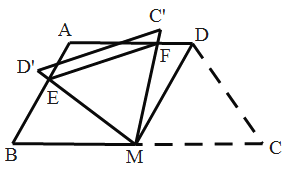
【題目】如圖，在四邊形
中，
，
，
，
是
的中點，將
繞點旋轉，當
（即
）與
交于一點
，
（
）同時與
交于一點
時，點，和點
構成
，在此過程中，周長的最小值是__________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，二次函數y=x2+bx+c的圖象與x軸交于A、B兩點，B點的坐標為（3，0），與y軸交于點C（0，﹣3），點P是直線BC下方拋物線上的任意一點，過點P作平行于y軸的直線PM，交線段BC于M，當△PCM是以PM為腰的等腰三角形時，點P的坐標是（ ）
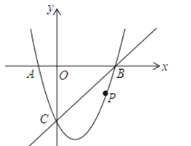
A.（2，-3）或（
+1，—2）B.（2，-3）或（，-1-2）
C.（2，-3）或（，-1-2）D.（2，-3）或（3-，2-4）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，四邊形ABCD是菱形，∠A=60°，AB=2，扇形BEF的半徑為2，圓心角為60°，則圖中陰影部分的面積是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
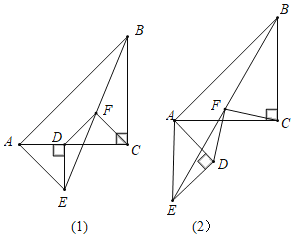
【題目】已知△ABC和△ADE都是等腰直角三角形，∠ACB＝∠ADE＝90°，點F為BE中點，連結DF，CF．
（1）如圖1，點D在AC上，請你判斷此時線段DF，CF的關系，并證明你的判斷；
（2）如圖2，在（1）的條件下將△ADE繞點A順時針旋轉45度時，若AD＝DE＝2，AB＝6，求此時線段CF的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】關于的一元二次方程x2+2x+k+1=0的實數解是x1和x2．
（1）求k的取值范圍；
（2）如果x1+x2﹣x1x2＜﹣1且k為整數，求k的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】“如圖1，在Rt△ABC中，∠ACB＝90°，CD⊥AB于點D．”這里，根據已學的相似三角形的知識，易證：
＝
．在圖1這個基本圖形的基礎上，繼續添加條件“如圖2，點E是直線AC上一動點，連接DE，過點D作FD⊥ED，交直線BC于點F，設＝
．”
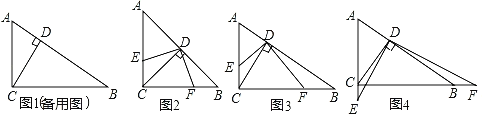
（1）探究發現：如圖②，若m＝n，點E在線段AC上，則
＝ ；
（2）數學思考：
①如圖3，若點E在線段AC上，則＝ （用含m，n的代數式表示）；
②當點E在直線AC上運動時，①中的結論是否仍然成立？請僅就圖4的情形給出證明；
（3）拓展應用：若AC＝
，BC＝2，DF＝4
，請直接寫出CE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
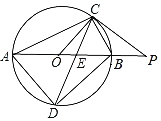
【題目】如圖，AB是⊙O的直徑，點C是⊙O上一點，連接AC、BC，過點C作∠BCP＝∠BAC，交AB的延長線于點P，弦CD平分∠ACB，交AB于點E，連接OC、AD、BD．
（1）求證：PC為⊙O的切線；
（2）若OC＝5，OE＝1，求PC的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com