
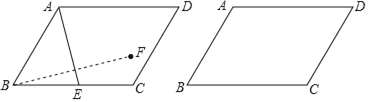
【題目】如圖,已知ABCD中,∠ABC=60°,AB=4,BC=m,E為BC邊上的動點,連結(jié)AE,作點B關(guān)于直線AE的對稱點F.
(1)若m=6,①當(dāng)點F恰好落在∠BCD的平分線上時,求BE的長;
②當(dāng)E、C重合時,求點F到直線BC的距離;
(2)當(dāng)點F到直線BC的距離d滿足條件:2![]() ﹣2≤d≤2
﹣2≤d≤2![]() +4,求m的取值范圍.
+4,求m的取值范圍.
【答案】(1)①BE=10﹣2![]() ;②
;②![]() ;(2)4
;(2)4![]() ﹣4≤m≤8+4
﹣4≤m≤8+4![]()
【解析】
(1)①過F作FT⊥BC于T,延長BA交∠BCD的平分線于G,連接BF,EF,AF,由平行四邊形性質(zhì)可得:△BCG,△CDH均為等邊三角形,AG=AH=2,再由B、F關(guān)于直線AE對稱,可證得:△CEF∽△GFA,再結(jié)合勾股定理可求得BE的長;
②設(shè)BF交AC于T,過T作TR⊥BC于R,過F作FH⊥BC于H,過A作AG⊥BC于G,可求得BG、AG、GH、AC,再由面積法可求得BT、BF,再證明△BTR∽△BFH,結(jié)合勾股定理即可求得點F到直線BC的距離;
(2)先找出d的最大值的情形,畫出圖形,由d的最大值可求得m的最大值再根據(jù)d的最小值求得m的最小值,即可得m的范圍.
解:(1)①如圖1,過F作FT⊥BC于T,延長BA交∠BCD的平分線于G,連接BF,EF,AF,
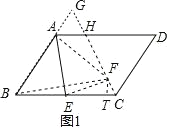
∵ABCD,
∴AB∥CD,AD∥BC,AB=CD,AD=BC,
∵∠ABC=60°,
∴∠BCD=120°,∠ADC=60°,
∵CG平分∠BCD,
∴∠BCG=∠DCG=60°
∴△BCG,△CDH均為等邊三角形,
∴CG=BC=BG=6,∠G=60°,DH=CD=4,
∴AG=AH=2,
∵B、F關(guān)于直線AE對稱,
∴AF=AB=4,EF=BE,∠AFE=∠ABC=60°,
∴∠AFG+∠CFE=120°,∠AFG+∠FAG=120°,
∴∠CFE=∠FAG,
∴△CEF∽△GFA,
∴![]() ,即:CF=
,即:CF=![]() EF,設(shè)BE=EF=x,則CF=
EF,設(shè)BE=EF=x,則CF=![]() x,
x,
∵∠CFT=30°,
∴CT=![]() CF=
CF=![]() x,FT=
x,FT=![]() x,
x,
∵ET2+FT2=EF2,
∴![]() ,
,
解得:x1=10+ ![]() (不符合題意,舍去),x2=10﹣
(不符合題意,舍去),x2=10﹣![]() ,
,
∴BE=10﹣2![]() ,
,
②如圖2,設(shè)BF交AC于T,過T作TR⊥BC于R,過F作FH⊥BC于H,過A作AG⊥BC于G,連接AF,FC,
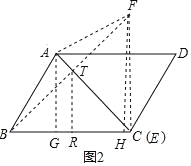
∵∠AGB=90°,∠ABC=60°,
∴∠BAG=30°
∴BG=![]() AB=2,AG=2
AB=2,AG=2![]() ,GC=BC﹣BG=4,
,GC=BC﹣BG=4,
∴AC=![]() ,
,
∵B、F關(guān)于AC對稱,
∴BF⊥AC,BT=TF,
由△ABC面積公式可得BTAC=AGBC,
即BT![]() =2
=2![]() ×6,
×6,
∴BT=![]() ,BF=
,BF=![]() ,
,
在Rt△BCT中,CT=![]() ,
,
∵TRBC=BTCT,即6TR=![]() ,
,
∴TR=![]() ,
,
∵TR⊥BC,FH⊥BC,
∴TR∥FH,
∴△BTR∽△BFH,
∴![]() ,
,
∴FH=2TR=![]() ,
,
故點F到直線BC的距離為![]()
(2)如圖3,作AG⊥BC于G,
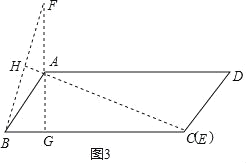
當(dāng)點F、A、G三點共線時,點F到直線BC的距離d最大,
此時點E與點C重合,FG=2 ![]() +4,
+4,
由(1)知,BG=2,AG=2 ![]() ,
,
∴BF=![]() ,
,
∴BH=![]() BF=
BF=![]() ,
,
∵∠BHC=∠BGF=90°,∠CBH=∠FBG,
∴△CBH∽△FBG,
∴![]() ,即
,即![]() ,
,
解得:m=8+4 ![]() ,
,
∴m的最大值為8+4 ![]() ,
,
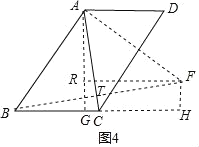
如圖4,作AG⊥BC于G,FH⊥BC于H,FR⊥AG于R,連接AF,
設(shè)BF交AC于T,
則AG=2 ![]() ,BG=2,CG=BC﹣BG=m-2,
,BG=2,CG=BC﹣BG=m-2,
此時點E與點C重合,FH=![]() ﹣2,
﹣2,
顯然,FHGR是矩形,
∴RG=FH=![]() ﹣2, AR=AG﹣RG=2,
﹣2, AR=AG﹣RG=2,
∵B、F關(guān)于AC對稱,
∴BF⊥AC,BT=TF,AF=AB=4,
∴RF=GH=![]() ,
,
∴BH=BG+GH=2+ ![]() ,
,
∴BF=![]() ,
,
∴BT=TF=![]() BF=2
BF=2![]() ,
,
∵△BCT∽△BFH,
∴![]() ,即
,即![]() ,
,
解得m=4 ![]() ﹣4,
﹣4,
∴m的最小值為4 ![]() ﹣4,
﹣4,
綜上所述,4![]() ﹣4≤m≤8+4
﹣4≤m≤8+4![]() .
.


 數(shù)學(xué)奧賽暑假天天練南京大學(xué)出版社系列答案
數(shù)學(xué)奧賽暑假天天練南京大學(xué)出版社系列答案 南大教輔搶先起跑暑假銜接教程南京大學(xué)出版社系列答案
南大教輔搶先起跑暑假銜接教程南京大學(xué)出版社系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,等腰![]() 中,
中,![]() ,
,![]() .動點
.動點![]() 在
在![]() 上以每分鐘5個單位長度的速度從
上以每分鐘5個單位長度的速度從![]() 點出發(fā)向
點出發(fā)向![]() 點移動,過
點移動,過![]() 作
作![]() 交
交![]() 邊于
邊于![]() 點,連結(jié)
點,連結(jié)![]() 、
、![]() .設(shè)
.設(shè)![]() 點移動的時間為
點移動的時間為![]() .
.
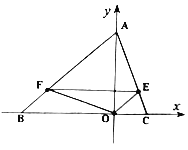
(1)求![]() 、
、![]() 兩點的坐標(biāo);
兩點的坐標(biāo);
(2)計算:當(dāng)![]() 面積最大時,
面積最大時,![]() 的值;
的值;
(3)在(2)的條件下,邊![]() 上是否還存在一個點
上是否還存在一個點![]() ,使得
,使得![]() ?若存在,請直接寫出
?若存在,請直接寫出![]() 點的坐標(biāo);若不存在,試說明理由.
點的坐標(biāo);若不存在,試說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,DEF分別為△ABC邊ACABBC上的點,∠A=∠1=∠C,DE=DF.下面的結(jié)論一定成立的是( )
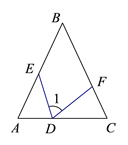
A. AE=FC B. AE=DE C. AE+FC=AC D. AD+FC=AB
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】現(xiàn)有一筆直的公路連接![]() 、
、![]() 兩地,甲車從
兩地,甲車從![]() 地駛往
地駛往![]() 地,速度為每小時60千米,同時乙車從
地,速度為每小時60千米,同時乙車從![]() 地駛往
地駛往![]() 地,速度為每小時80千米.途中甲車發(fā)生故障,于是停車修理了2.5小時,修好后立即開車駛往
地,速度為每小時80千米.途中甲車發(fā)生故障,于是停車修理了2.5小時,修好后立即開車駛往![]() 地.設(shè)甲車行駛的時間為
地.設(shè)甲車行駛的時間為![]() ,兩車之間的距離為
,兩車之間的距離為![]() .已知
.已知![]() 與
與![]() 的函數(shù)關(guān)系的部分圖像如圖所示.
的函數(shù)關(guān)系的部分圖像如圖所示.
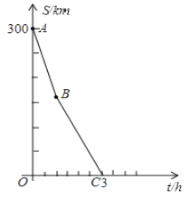
(1)直接寫出![]() 點的實際意義.
點的實際意義.
(2)問:甲車出發(fā)幾小時后發(fā)生故障?
(3)將![]() 與
與![]() 的函數(shù)圖象補充完整.(請對畫出的圖象用數(shù)據(jù)作適當(dāng)?shù)臉?biāo)注)
的函數(shù)圖象補充完整.(請對畫出的圖象用數(shù)據(jù)作適當(dāng)?shù)臉?biāo)注)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩人要某風(fēng)景區(qū)游玩,每天某一時段開往該景區(qū)有三輛汽車(票價相同),但是他們不清楚這三輛車的舒適程度,也不知道汽車開來的順序,兩人采用了不同的乘車方案:
甲無論如何總是上開來的第一輛車,而乙則是先觀察后上車,當(dāng)?shù)谝惠v車開來時,他不上車,而是仔細(xì)觀察車輛的舒適狀況,如果第二輛車狀況比第一輛好,他就上第二輛車,如果第二輛不比第一輛好,他就上第三輛車.這三輛車的舒適程度為上、中、下三等,請解決下面的問題:
(1)請用畫樹形圖或列表的方法分析這三輛車出現(xiàn)的先后順序,寫出所有可能的結(jié)果;(用上中下表示)
(2)分析甲、乙兩人采用的方案,誰的方案使自己坐上上等車的可能性大,說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,學(xué)校教學(xué)樓對面是一幢實驗樓,小朱在教學(xué)樓的窗口C測得實驗樓頂部D的仰角為20°,實驗樓底部B的俯角為30°,量得教學(xué)樓與實驗樓之間的距離AB=30m.求實驗樓的高BD.(結(jié)果精確到1m.參考數(shù)據(jù)tan20°≈0.36,sin20°≈0.34,cos20°≈0.94,![]()
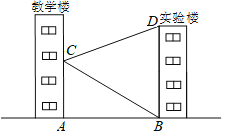
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】解決問題.
學(xué)校要購買A,B兩種型號的足球,按體育器材門市足球銷售價格(單價)計算:若買2個A型足球和3個B型足球,則要花費370元,若買3個A型足球和1個B型足球,則要花費240元.
(1)求A,B兩種型號足球的銷售價格各是多少元/個?
(2)學(xué)校擬向該體育器材門市購買A,B兩種型號的足球共20個,且費用不低于1300元,不超過1500元,則有哪幾種購球方案?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,點![]() 分別在
分別在![]() 兩邊上,且
兩邊上,且![]() ,以
,以![]() 為直徑作半圓
為直徑作半圓![]() ,點
,點![]() 是半圓
是半圓![]() 的中點
的中點
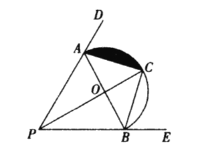
(1)連接![]() ,求證:
,求證: ![]() ;
;
(2)若![]() ,
, ![]() ,求陰影部分面積
,求陰影部分面積
(3)若點![]() 是
是![]() 的外心,判斷四邊形
的外心,判斷四邊形![]() 的形狀,并說明理由
的形狀,并說明理由
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】改革開放40年以來,城鄉(xiāng)居民生活水平持續(xù)快速提升.居民教育、文化和娛樂消費支出持續(xù)增長,已經(jīng)成為居民各項消費支出中僅次于居住、食品煙酒、交通通信后的第四大消費支出.下圖為北京市統(tǒng)計局發(fā)布的2017年和2018年我市居民人均教育、文化和娛樂消費支出的折線圖:
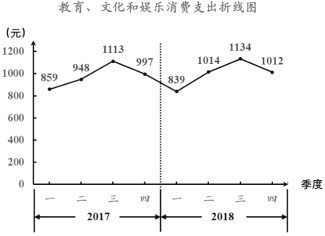
說明:在統(tǒng)計學(xué)中,同比是指本期統(tǒng)計數(shù)據(jù)與上一年同期統(tǒng)計數(shù)據(jù)相比較,例如2018年第二季度與2017年第二季度相比較;環(huán)比是指本期統(tǒng)計數(shù)據(jù)與上期統(tǒng)計數(shù)據(jù)相比較,例如2018年第二季度與2018年第一季度相比較.
根據(jù)上述信息,下列結(jié)論中錯誤的是( ).
A.2017年第二季度環(huán)比有所提高B.2017年第四季度環(huán)比有所下降
C.2018年第一季度同比有所提高D.2017和2018年支出最高的都是第三季度
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com