
【題目】某出租汽車公司計劃購買![]() 型和
型和![]() 型兩種節能汽車,若購買
型兩種節能汽車,若購買![]() 型汽車
型汽車![]() 輛,
輛,![]() 型汽車
型汽車![]() 輛,共需
輛,共需![]() 萬元;若購買
萬元;若購買![]() 型汽車
型汽車![]() 輛,
輛,![]() 型汽車
型汽車![]() 輛,共需
輛,共需![]() 萬元.
萬元.
(1)![]() 型和
型和![]() 型汽車每輛的價格分別是多少萬元?
型汽車每輛的價格分別是多少萬元?
(2)該公司計劃購買![]() 型和
型和![]() 型兩種汽車共
型兩種汽車共![]() 輛,費用不超過
輛,費用不超過![]() 萬元,且
萬元,且![]() 型汽車的數量少于
型汽車的數量少于![]() 型汽車的數量,請你給出費用最省的方案,并求出該方案所需費用.
型汽車的數量,請你給出費用最省的方案,并求出該方案所需費用.
【答案】(1)![]() 型汽車每輛的價格為
型汽車每輛的價格為![]() 萬元,
萬元,![]() 型汽車每輛的價格為
型汽車每輛的價格為![]() 萬元;(2)費用最省的方案是購買
萬元;(2)費用最省的方案是購買![]() 型汽車
型汽車![]() 輛,
輛,![]() 型汽車
型汽車![]() 輛,該方案所需費用為
輛,該方案所需費用為![]() 萬元.
萬元.
【解析】
(1)設![]() 型汽車每輛的價格為
型汽車每輛的價格為![]() 萬元,
萬元,![]() 型汽車每輛的價格為
型汽車每輛的價格為![]() 萬元,根據購買
萬元,根據購買![]() 型汽車
型汽車![]() 輛,
輛,![]() 型汽車
型汽車![]() 輛,共需
輛,共需![]() 萬元;購買
萬元;購買![]() 型汽車
型汽車![]() 輛,
輛,![]() 型汽車
型汽車![]() 輛,共需
輛,共需![]() 萬元,列方程組進行求解即可;
萬元,列方程組進行求解即可;
(2)設購買![]() 型汽車
型汽車![]() 輛,則購買
輛,則購買![]() 型汽車
型汽車![]() 輛,根據總費用不超過
輛,根據總費用不超過![]() 萬元,且
萬元,且![]() 型汽車的數量少于
型汽車的數量少于![]() 型汽車的數量,列不等式組進行求解得出購買方案,然后再討論即可得.
型汽車的數量,列不等式組進行求解得出購買方案,然后再討論即可得.
(1)設![]() 型汽車每輛的價格為
型汽車每輛的價格為![]() 萬元,
萬元,![]() 型汽車每輛的價格為
型汽車每輛的價格為![]() 萬元,
萬元,
由題意得:
![]() ,
,
解得![]() ,
,
答:![]() 型汽車每輛的價格為
型汽車每輛的價格為![]() 萬元,
萬元,![]() 型汽車每輛的價格為
型汽車每輛的價格為![]() 萬元;
萬元;
(2)設購買![]() 型汽車
型汽車![]() 輛,則購買
輛,則購買![]() 型汽車
型汽車![]() 輛,
輛,
由題意得:![]() ,
,
解得:![]() ,因為
,因為![]() 是整數,
是整數,
所以![]() 或
或![]() ,
,
當![]() 時,該方案所需費用為:
時,該方案所需費用為:![]() 萬元;
萬元;
當![]() 時,該方案所需費用為:
時,該方案所需費用為:![]() 萬元,
萬元,
答:費用最省的方案是購買![]() 型汽車
型汽車![]() 輛,
輛,![]() 型汽車
型汽車![]() 輛,該方案所需費用為
輛,該方案所需費用為![]() 萬元.
萬元.


科目:初中數學 來源: 題型:
【題目】教室里的飲水機接通電源就進入自動程序,開機加熱時每分鐘上升10℃,加熱到100℃停止加熱,水溫開始下降,此時水溫![]() (℃)與開機后用時
(℃)與開機后用時![]() (
(![]() )成反比例關系,直至水溫降至30℃,飲水機關機,飲水機關機后即刻自動開機,重復上述自動程序.若在水溫為30℃時接通電源,水溫
)成反比例關系,直至水溫降至30℃,飲水機關機,飲水機關機后即刻自動開機,重復上述自動程序.若在水溫為30℃時接通電源,水溫![]() (℃)與時間
(℃)與時間![]() (
(![]() )的關系如圖所示:
)的關系如圖所示:
(1)分別寫出水溫上升和下降階段![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(2)怡萱同學想喝高于50℃的水,請問她最多需要等待多長時間?

查看答案和解析>>
科目:初中數學 來源: 題型:
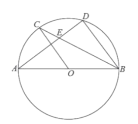
【題目】如圖,![]() 為⊙
為⊙![]() 的直徑,
的直徑,![]() ,
,![]() 為圓上的兩點,
為圓上的兩點,![]() ,弦
,弦![]() ,
,![]() 相交于點
相交于點![]() ,
,
(1)求證:![]()
(2)若![]() ,
,![]() ,求⊙
,求⊙![]() 的半徑;
的半徑;
(3)在(2)的條件下,過點![]() 作⊙
作⊙![]() 的切線,交
的切線,交![]() 的延長線于點
的延長線于點![]() ,過點
,過點![]() 作
作![]() 交⊙
交⊙![]() 于
于![]() ,
, ![]() 兩點(點
兩點(點![]() 在線段
在線段![]() 上),求
上),求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
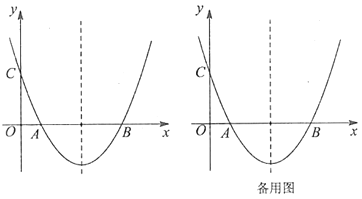
【題目】如圖,拋物線![]() 經點
經點![]() ,與
,與![]() 軸相交于點
軸相交于點![]() .
.
(1)求拋物線的解析式;
(2)定義:平面上的任一點到二次函數圖象上與它橫坐標相同的點的距離,稱為點到二次函數圖象的垂直距離.如:點![]() 到二次函數圖象的垂直距離是線段
到二次函數圖象的垂直距離是線段![]() 的長.已知點
的長.已知點![]() 為拋物線對稱軸上的一點,且在
為拋物線對稱軸上的一點,且在![]() 軸上方,點
軸上方,點![]() 為平面內一點,當以
為平面內一點,當以![]() 為頂點的四邊形是邊長為4的菱形時,請求出點
為頂點的四邊形是邊長為4的菱形時,請求出點![]() 到二次函數圖象的垂直距離.
到二次函數圖象的垂直距離.
(3)在(2)中,當點![]() 到二次函數圖象的垂直距離最小時,在
到二次函數圖象的垂直距離最小時,在![]() 為頂點的菱形內部是否存在點
為頂點的菱形內部是否存在點![]() ,使得
,使得![]() 之和最小,若存在,請求出最小值;若不存在,請說明理由.
之和最小,若存在,請求出最小值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某養殖場為了響應黨中央的扶貧政策,今年起采用“場內+農戶”養殖模式,同時加強對蛋雞的科學管理,蛋雞的產蛋率不斷提高,三月份和五月份的產蛋量分別是2.5萬kg與3.6萬kg,現假定該養殖場蛋雞產蛋量的月增長率相同.
(1)求該養殖場蛋雞產蛋量的月平均增長率;
(2)假定當月產的雞蛋當月在各銷售點全部銷售出去,且每個銷售點每月平均銷售量最多為0.32萬kg.如果要完成六月份的雞蛋銷售任務,那么該養殖場在五月份已有的銷售點的基礎上至少再增加多少個銷售點?
查看答案和解析>>
科目:初中數學 來源: 題型:
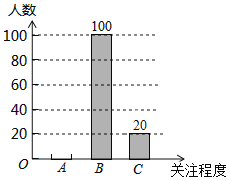
【題目】湖南省作為全國第三批啟動高考綜合改革的省市之一,從2018年秋季入學的高中一年級學生開始實施高考綜合改革.深化高考綜合改革,承載著廣大考生的美好期盼,事關千家萬戶的切身利益,社會關注度高.為了了解我市某小區居民對此政策的關注程度,某數學興趣小組隨機采訪了該小區部分居民,根據采訪情況制做了如統計圖表:
關注程度 | 頻數 | 頻率 |
A.高度關注 | m | 0.4 |
B.一般關注 | 100 | 0.5 |
C.沒有關注 | 20 | n |
(1)根據上述統計圖表,可得此次采訪的人數為 ,m= ,n= .
(2)根據以上信息補全圖中的條形統計圖.
(3)請估計在該小區1500名居民中,高度關注新高考政策的約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
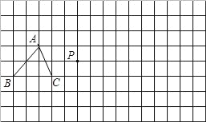
【題目】在下面16×8的正方形網格中,每個小正方形的邊長為1個單位,△ABC是格點三角形(頂點在網格交點處),請你畫出:
(1)△ABC關于點P的位似△A′B′C′,且位似比為1:2;
(2)以A.B.C.D為頂點的所有格點平行四邊形ABCD的頂點D
.
查看答案和解析>>
科目:初中數學 來源: 題型:
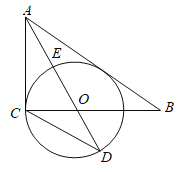
【題目】如圖1,在直角△ABC中,∠ACB=90°,AO是△ABC的角平分線,以O為圓心,OC為半徑作圓O
(1)求證:AB是⊙O的切線;
(2)已知AO交圓O于點E,延長AO交圓O于點D,tan∠D=![]() ,求
,求![]() 的值;
的值;
(3)如圖2,在(2)條件下,若AB與⊙O的切點為點F,連接CF交AD于點G,設⊙O的半徑為3,求CF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】類比等腰三角形的定義,我們定義:有三條邊相等的凸四邊形叫做“準等邊四邊形”
(1)已知:如圖1,在“準等邊四邊形”ABCD中,BC≠AB,BD⊥CD,AB=3,BD=4,求BC的長;
(2)在探究性質時,小明發現一個結論:對角線互相垂直的“準等邊四邊形”是菱形.請你判斷此結論是否正確,若正確,請說明理由;若不正確,請舉出反例;
(3)如圖2,在△ABC中,AB=AC,∠BAC=90°,BC=2.在AB的垂直平分線上是否存在點P使得以A,B,C,P為頂點的四邊形為“準等邊四邊形”?若存在,請求出該“準等邊四邊形”的面積;若不存在,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com