
【題目】如圖,以x=1為對(duì)稱(chēng)軸的拋物線(xiàn)y=ax2+bx+c的圖象與x軸交于點(diǎn)A,點(diǎn)B(﹣1,0),與y軸交于點(diǎn)C(0,4),作直線(xiàn)AC.
(1)求拋物線(xiàn)解析式;
(2)點(diǎn)P在拋物線(xiàn)的對(duì)稱(chēng)軸上,且到直線(xiàn)AC和x軸的距離相等,設(shè)點(diǎn)P的縱坐標(biāo)為m,求m的值;
(3)點(diǎn)M在y軸上且位于點(diǎn)C上方,點(diǎn)N在直線(xiàn)AC上,點(diǎn)Q為第一象限內(nèi)拋物線(xiàn)上一點(diǎn),若以點(diǎn)C、M、N、Q為頂點(diǎn)的四邊形是菱形,請(qǐng)直接寫(xiě)出點(diǎn)Q的坐標(biāo).
【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2)m的值為1或﹣4;(3)點(diǎn)Q的坐標(biāo)為(1,
x+4;(2)m的值為1或﹣4;(3)點(diǎn)Q的坐標(biāo)為(1,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)先利用拋物線(xiàn)的對(duì)稱(chēng)性得到A(3,0),則可設(shè)交點(diǎn)式y=a(x+1)(x﹣3),然后把C點(diǎn)坐標(biāo)代入求出a即可;
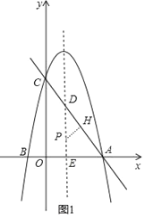
(2)先利用待定系數(shù)法其出直線(xiàn)AC的解析式為y=﹣![]() x+4;令對(duì)稱(chēng)軸與直線(xiàn)AC交于點(diǎn)D,與x軸交于點(diǎn)E,作PH⊥AD于H,如圖1,易得D(1,
x+4;令對(duì)稱(chēng)軸與直線(xiàn)AC交于點(diǎn)D,與x軸交于點(diǎn)E,作PH⊥AD于H,如圖1,易得D(1,![]() ),利用勾股定理計(jì)算出AD=
),利用勾股定理計(jì)算出AD=![]() ,設(shè)P(1,m),則PD=
,設(shè)P(1,m),則PD=![]() ﹣m,PH=PE=|m|,證明△DPH∽△DAE,利用相似比得到
﹣m,PH=PE=|m|,證明△DPH∽△DAE,利用相似比得到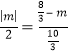 ,然后解方程可得到m的值;
,然后解方程可得到m的值;
(3)設(shè)Q(t,﹣![]() x2+
x2+![]() x+4)(0<t<4),討論:當(dāng)CM為對(duì)角線(xiàn)時(shí),四邊形CQMN為菱形,如圖2,根據(jù)菱形的性質(zhì)判定點(diǎn)N和Q關(guān)于y軸對(duì)稱(chēng),則N(﹣t,﹣
x+4)(0<t<4),討論:當(dāng)CM為對(duì)角線(xiàn)時(shí),四邊形CQMN為菱形,如圖2,根據(jù)菱形的性質(zhì)判定點(diǎn)N和Q關(guān)于y軸對(duì)稱(chēng),則N(﹣t,﹣![]() x2+
x2+![]() x+4),然后把N(﹣t,﹣
x+4),然后把N(﹣t,﹣![]() x2+
x2+![]() x+4)代入y=﹣
x+4)代入y=﹣![]() x+4得t的方程,從而解方程求出t得到此時(shí)Q點(diǎn)坐標(biāo);當(dāng)CM為菱形的邊時(shí),四邊形CNQM為菱形,如圖3,利用菱形的性質(zhì)得NQ∥y軸,NQ=NC,則N(t,﹣
x+4得t的方程,從而解方程求出t得到此時(shí)Q點(diǎn)坐標(biāo);當(dāng)CM為菱形的邊時(shí),四邊形CNQM為菱形,如圖3,利用菱形的性質(zhì)得NQ∥y軸,NQ=NC,則N(t,﹣![]() t+4),所以NQ=﹣
t+4),所以NQ=﹣![]() t2+4t,再根據(jù)兩點(diǎn)間的距離公式計(jì)算出CN=
t2+4t,再根據(jù)兩點(diǎn)間的距離公式計(jì)算出CN=![]() t,所以﹣
t,所以﹣![]() t2+4t=
t2+4t=![]() t,從而解方程求出t得到此時(shí)Q點(diǎn)坐標(biāo).
t,從而解方程求出t得到此時(shí)Q點(diǎn)坐標(biāo).
解:(1)∵點(diǎn)A與點(diǎn)B(﹣1,0)關(guān)于直線(xiàn)x=1對(duì)稱(chēng),
∴A(3,0),
設(shè)拋物線(xiàn)解析式為y=a(x+1)(x﹣3),
把C(0,4)代入得a1(﹣3)=4,解得a=﹣![]() ,
,
∴拋物線(xiàn)解析式為y=﹣![]() (x+1)(x﹣3),即y=﹣
(x+1)(x﹣3),即y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)設(shè)直線(xiàn)AC的解析式為y=kx+p,
把A(3,0),C(0,4)代入得![]() ,解得
,解得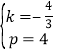 ,
,
∴直線(xiàn)AC的解析式為y=﹣![]() x+4;
x+4;
令對(duì)稱(chēng)軸與直線(xiàn)AC交于點(diǎn)D,與x軸交于點(diǎn)E,作PH⊥AD于H,如圖1,
當(dāng)x=1時(shí),y=﹣![]() x+4=
x+4=![]() ,則D(1,
,則D(1,![]() ),
),
∴DE=![]() ,
,
在Rt△ADE中,AD=![]() =
=![]() ,
,
設(shè)P(1,m),則PD=![]() ﹣m,PH=PE=|m|,
﹣m,PH=PE=|m|,
∵∠PDH=∠ADE,
∴△DPH∽△DAE,
∴![]() ,即
,即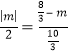 ,解得m=1或m=﹣4,
,解得m=1或m=﹣4,
即m的值為1或﹣4;
(3)設(shè)Q(t,﹣![]() t2+
t2+![]() t+4)(0<t<4),
t+4)(0<t<4),
當(dāng)CM為對(duì)角線(xiàn)時(shí),四邊形CQMN為菱形,如圖2,則點(diǎn)N和Q關(guān)于y軸對(duì)稱(chēng),
∴N(﹣t,﹣![]() t2+
t2+![]() t+4),
t+4),
把N(﹣t,﹣![]() t2+
t2+![]() t+4)代入y=﹣
t+4)代入y=﹣![]() x+4得
x+4得![]() t+4=﹣
t+4=﹣![]() t2+
t2+![]() t+4,解得t1=0(舍去),t2=1,此時(shí)Q點(diǎn)坐標(biāo)為(1,
t+4,解得t1=0(舍去),t2=1,此時(shí)Q點(diǎn)坐標(biāo)為(1,![]() );
);
當(dāng)CM為菱形的邊時(shí),四邊形CNQM為菱形,如圖3,則NQ∥y軸,NQ=NC,
∴N(t,﹣![]() t+4),
t+4),
∴NQ=﹣![]() t2+
t2+![]() t+4﹣(﹣
t+4﹣(﹣![]() t+4)=﹣
t+4)=﹣![]() t2+4t,
t2+4t,
而CN2=t2+(﹣![]() t+4﹣4)2=
t+4﹣4)2=![]() t2,即CN=
t2,即CN=![]() t,
t,
∴﹣![]() t2+4t=
t2+4t=![]() t,解得t1=0(舍去),t2=
t,解得t1=0(舍去),t2=![]() ,此時(shí)Q點(diǎn)坐標(biāo)為(
,此時(shí)Q點(diǎn)坐標(biāo)為(![]() ,
,![]() ),
),
綜上所述,點(diǎn)Q的坐標(biāo)為(1,![]() )或(
)或(![]() ,
,![]() ).
).


 備戰(zhàn)中考寒假系列答案
備戰(zhàn)中考寒假系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
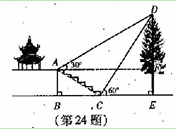
【題目】(本題7分)如圖,某校綜合實(shí)踐活動(dòng)小組的同學(xué)欲測(cè)量公園內(nèi)一棵樹(shù)DE的高度.他們?cè)谶@棵樹(shù)正前方一座樓亭前的臺(tái)階上A點(diǎn)處測(cè)得樹(shù)頂端D的仰角為30°,朝著這棵樹(shù)的方向走到臺(tái)階下的點(diǎn)C處,測(cè)得樹(shù)頂端D的仰角為60°.已知A點(diǎn)的高度AB為2米,臺(tái)階AC的坡度為![]() (即AB:BC=
(即AB:BC=![]() ),且B、C、E三點(diǎn)在同一條盲線(xiàn)上。請(qǐng)根據(jù)以上殺件求出樹(shù)DE的高度(測(cè)傾器的高度忽略不計(jì)).
),且B、C、E三點(diǎn)在同一條盲線(xiàn)上。請(qǐng)根據(jù)以上殺件求出樹(shù)DE的高度(測(cè)傾器的高度忽略不計(jì)).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
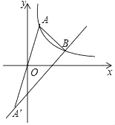
【題目】平面直角坐標(biāo)系xOy中,橫坐標(biāo)為a的點(diǎn)A在反比例函數(shù)y1=![]() (x>0)的圖象上.點(diǎn)A與點(diǎn)A關(guān)于點(diǎn)O對(duì)稱(chēng),一次函數(shù)y2=mx+n的圖象經(jīng)過(guò)點(diǎn)A.
(x>0)的圖象上.點(diǎn)A與點(diǎn)A關(guān)于點(diǎn)O對(duì)稱(chēng),一次函數(shù)y2=mx+n的圖象經(jīng)過(guò)點(diǎn)A.
(1)設(shè)a=2,點(diǎn)B(4,2)在函數(shù)y1,y2的圖象上.
①分別求函數(shù)y1,y2的表達(dá)式;
②直接寫(xiě)出使y1>y2>0成立的x的范圍.
(2)如圖,設(shè)函數(shù)y1,y2的圖象相交于點(diǎn)B,點(diǎn)B的橫坐標(biāo)為3a,△AA′B的面積為16,求k的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
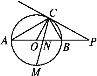
【題目】如圖,AB是☉O的直徑,點(diǎn)C在☉O上,過(guò)點(diǎn)C的直線(xiàn)與AB的延長(zhǎng)線(xiàn)交于點(diǎn)P,∠COB=2∠PCB.
(1)求證:PC是☉O的切線(xiàn);
(2)點(diǎn)M是弧AB的中點(diǎn),CM交AB于點(diǎn)N,若MN·MC=8,求☉O的直徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】水果店張阿姨以每斤2元的價(jià)格購(gòu)進(jìn)某種水果若干斤,然后以每斤4元的價(jià)格出售,每天可售出100斤.通過(guò)調(diào)查發(fā)現(xiàn),這種水果每斤的售價(jià)每降低0.1元,每天可多售出20斤.為了保證每天至少售出260斤,張阿姨決定降價(jià)銷(xiāo)售.
(1)若將這種水果每斤的售價(jià)降低x元,則每天的銷(xiāo)售量是 斤(用含x的代數(shù)式表示);
(2)銷(xiāo)售這種水果要想每天盈利300元,張阿姨需將每斤的售價(jià)降低多少元?
(3)當(dāng)每斤的售價(jià)定為多少元時(shí),每天獲利最大?最大值為多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】每年的3月22日為聯(lián)合國(guó)確定的“世界水日”,某社區(qū)為了宣傳節(jié)約用水,從本社區(qū)1000戶(hù)家庭中隨機(jī)抽取部分家庭,調(diào)查他們每月的用水量,并將調(diào)查的結(jié)果繪制成如下兩幅尚不完整的統(tǒng)計(jì)圖(每組數(shù)據(jù)包括右端點(diǎn)但不包括左端點(diǎn)),請(qǐng)你根據(jù)統(tǒng)計(jì)圖解答下列問(wèn)題:
(1)此次抽樣調(diào)查的樣本容量是 ;
(2)補(bǔ)全頻數(shù)分布直方圖,求扇形圖中“6噸﹣﹣9噸”部分的圓心角的度數(shù);
(3)如果自來(lái)水公司將基本月用水量定為每戶(hù)每月12噸,不超過(guò)基本月用水量的部分享受基本價(jià)格,超出基本月用水量的部分實(shí)行加價(jià)收費(fèi),那么該社會(huì)用戶(hù)中約有多少戶(hù)家庭能夠全部享受基本價(jià)格?

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知二次函數(shù)y=﹣2x2+bx+c的圖象經(jīng)過(guò)點(diǎn)A(0,4)和B(1,﹣2).
(1)求此拋物線(xiàn)的解析式;
(2)求此拋物線(xiàn)的對(duì)稱(chēng)軸和頂點(diǎn)坐標(biāo);
(3)設(shè)拋物線(xiàn)的頂點(diǎn)為C,試求△CAO的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,以AD為直徑的半圓O經(jīng)過(guò)Rt△ABC斜邊AB的兩個(gè)端點(diǎn),交直角邊AC于點(diǎn)E,B,E是半圓弧的三等分點(diǎn),弧AB的長(zhǎng)為![]() ,則圖中陰影部分的面積為( )
,則圖中陰影部分的面積為( )

A. 6![]() ﹣
﹣![]() B. 9
B. 9![]() ﹣
﹣![]() C.
C. ![]() ﹣
﹣![]() D. 6
D. 6![]() ﹣
﹣![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知:如圖,在山腳的A處測(cè)得山頂D的仰角為45°,沿著坡度為30°的斜角前進(jìn)400米處到B處(即∠BAC=30°,AB=400米),測(cè)得D的仰角為60°,求山的高度CD.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com