
【題目】如圖,直線y=﹣x﹣4與拋物線y=ax2+bx+c相交于A,B兩點(diǎn),其中A,B兩點(diǎn)的橫坐標(biāo)分別為﹣1和﹣4,且拋物線過原點(diǎn).
(1)求拋物線的解析式;
(2)在坐標(biāo)軸上是否存在點(diǎn)C,使△ABC為等腰三角形?若存在,求出點(diǎn)C的坐標(biāo),若不存在,請(qǐng)說明理由;
(3)若點(diǎn)P是線段AB上不與A,B重合的動(dòng)點(diǎn),過點(diǎn)P作PE∥OA,與拋物線第三象限的部分交于一點(diǎn)E,過點(diǎn)E作EG⊥x軸于點(diǎn)G,交AB于點(diǎn)F,若S△BGF=3S△EFP,求![]() 的值.
的值.

【答案】(1)拋物線解析式為y=x2+4x;(2)存在滿足條件的點(diǎn)C,其坐標(biāo)為(0,﹣3﹣![]() )或(0,﹣3﹣
)或(0,﹣3﹣![]() )或(﹣4+3
)或(﹣4+3![]() ,0)或(﹣4﹣3
,0)或(﹣4﹣3![]() ,0)或(﹣1,0)或(0,1)或(2,0)或(0,
,0)或(﹣1,0)或(0,1)或(2,0)或(0, ![]() )或(0,﹣
)或(0,﹣![]() );(3)
);(3)![]() .
.
【解析】試題分析:(1)由直線解析式可分別求得A、B兩點(diǎn)的坐標(biāo),利用待定系數(shù)法可求得拋物線解析式;
(2)當(dāng)AB=AC時(shí),點(diǎn)C在y軸上,可表示出AC的長(zhǎng)度,可求得其坐標(biāo);當(dāng)AB=BC時(shí),可知點(diǎn)C在x軸上,可表示出BC的長(zhǎng)度,可求得其坐標(biāo);當(dāng)AC=BC時(shí)點(diǎn)C在線段AB的垂直平分線與坐標(biāo)軸的交點(diǎn)處,可求得線段AB的中點(diǎn)的坐標(biāo),可求得垂直平分線的解析式,則可求得C點(diǎn)坐標(biāo);
(3)過點(diǎn)P作PQ⊥EF,交EF于點(diǎn)Q,過點(diǎn)A作AD⊥x軸于點(diǎn)D,可證明△PQE∽△ODA,可求得EQ=3PQ,再結(jié)合F點(diǎn)在直線AB上,可求得FQ=PQ,則可求得EF=4PQ,利用三角形的面積的關(guān)系可求得GF與PQ的關(guān)系,則可求得比值.
試題解析:(1)∵A,B兩點(diǎn)在直線y=﹣x﹣4上,且橫坐標(biāo)分別為﹣1、﹣4,
∴A(﹣1,﹣3),B(﹣4,0),
∵拋物線過原點(diǎn),
∴c=0,
把A、B兩點(diǎn)坐標(biāo)代入拋物線解析式可得![]() ,解得
,解得![]() ,
,
∴拋物線解析式為y=x2+4x;
(2)∵△ABC為等腰三角形,
∴有AB=AC、AB=BC和CA=CB三種情況,
①當(dāng)AB=AC時(shí),當(dāng)點(diǎn)C在y軸上,設(shè)C(0,y),
則AB=![]() =3
=3![]() ,AC=
,AC=![]() ,
,
∴3![]() =
=![]() ,解得y=﹣3﹣
,解得y=﹣3﹣![]() 或y=﹣3+
或y=﹣3+![]() ,
,
∴C(0,﹣3﹣![]() )或(0,﹣3﹣
)或(0,﹣3﹣![]() );
);
當(dāng)點(diǎn)C在x軸上時(shí),設(shè)C(x,0),則AC=![]() ,
,
∴![]() =3
=3![]() ,解得x=﹣4或x=2,當(dāng)x=﹣4時(shí),B、C重合,舍去,
,解得x=﹣4或x=2,當(dāng)x=﹣4時(shí),B、C重合,舍去,
∴C(2,0);
②當(dāng)AB=BC時(shí),當(dāng)點(diǎn)C在x軸上,設(shè)C(x,0),
則有AB=3![]() ,BC=|x+4|,
,BC=|x+4|,
∴|x+4|=3![]() ,解得x=﹣4+3
,解得x=﹣4+3![]() 或x=﹣4﹣3
或x=﹣4﹣3![]() ,
,
∴C(﹣4+3![]() ,0)或(﹣4﹣3
,0)或(﹣4﹣3![]() ,0);
,0);
當(dāng)點(diǎn)C在y軸上,設(shè)C(0,y),則BC=![]() ,
,
∴![]() =3
=3![]() ,解得y=
,解得y=![]() 或y=﹣
或y=﹣![]() ,
,
∴C(0, ![]() )或(0,﹣
)或(0,﹣![]() );
);
③當(dāng)CB=CA時(shí),則點(diǎn)C在線段AB的垂直平分線與y軸的交點(diǎn)處,
∵A(﹣1,﹣3),B(﹣4,0),
∴線段AB的中點(diǎn)坐標(biāo)為(﹣![]() ,﹣
,﹣![]() ),
),
設(shè)線段AB的垂直平分線的解析式為y=x+d,
∴﹣![]() =﹣
=﹣![]() +d,解得d=1,
+d,解得d=1,
∴線段AB的垂直平分線的解析式為y=x+1,
令x=0可得y=1,令y=0可求得x=﹣1,
∴C(﹣1,0)或(0,1);
綜上可知存在滿足條件的點(diǎn)C,其坐標(biāo)為(0,﹣3﹣![]() )或(0,﹣3﹣
)或(0,﹣3﹣![]() )或(﹣4+3
)或(﹣4+3![]() ,0)或(﹣4﹣3
,0)或(﹣4﹣3![]() ,0)或(﹣1,0)或(0,1)或(2,0)或(0,
,0)或(﹣1,0)或(0,1)或(2,0)或(0, ![]() )或(0,﹣
)或(0,﹣![]() );
);
(3)過點(diǎn)P作PQ⊥EF,交EF于點(diǎn)Q,過點(diǎn)A作AD⊥x軸于點(diǎn)D,
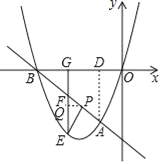
∵PE∥OA,GE∥AD,
∴∠OAD=∠PEG,∠PQE=∠ODA=90°,
∴△PQE∽△ODA,
∴![]() =3,即EQ=3PQ,
=3,即EQ=3PQ,
∵直線AB的解析式為y=﹣x﹣4,
∴∠ABO=45°=∠PFQ,
∴PQ=FQ,BG=GF,
∴EF=4PQ,
∴GE=GF+4PQ,
∵S△BGF=3S△EFP,
∴![]() GF2=3×
GF2=3×![]() ×4PQ2,
×4PQ2,
∴GF=2![]() PQ,
PQ,
∴![]() .
.


 小學(xué)教材全測(cè)系列答案
小學(xué)教材全測(cè)系列答案 小學(xué)數(shù)學(xué)口算題卡脫口而出系列答案
小學(xué)數(shù)學(xué)口算題卡脫口而出系列答案 優(yōu)秀生應(yīng)用題卡口算天天練系列答案
優(yōu)秀生應(yīng)用題卡口算天天練系列答案 浙江之星課時(shí)優(yōu)化作業(yè)系列答案
浙江之星課時(shí)優(yōu)化作業(yè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】下列語句:①全等三角形的周長(zhǎng)相等.②面積相等的三角形是全等三角形.③若成軸對(duì)稱的兩個(gè)圖形中的對(duì)稱線段所在直線相交,則這個(gè)交點(diǎn)一定在對(duì)稱軸上.④全等三角形的所有邊相等.其中正確的有( )
A. 0個(gè) B. 1個(gè) C. 2個(gè) D. 3個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,在△ABC中,∠BAC=90°,AB⊥AC,AB=3,BC=5,EF垂直平分BC,點(diǎn)P為直線EF上的任一點(diǎn),則AP+BP的最小值是 . 
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】下列命題中,是真命題的是( )
A. 任何數(shù)都有平方根 B. 只有正數(shù)才有平方根
C. 負(fù)數(shù)沒有立方根 D. 存在算術(shù)平方根等于本身的數(shù)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,直線l1的函數(shù)表達(dá)式為y1=﹣3x+3,且l1與x軸交于點(diǎn)D,直線l2:y2=kx+b經(jīng)過點(diǎn)A,B,與直線l1交于點(diǎn)C.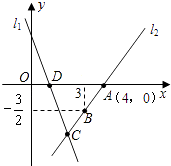
(1)求直線l2的函數(shù)表達(dá)式及C點(diǎn)坐標(biāo);
(2)求△ADC的面積;
(3)當(dāng)x滿足何值時(shí),y1>y2;(直接寫出結(jié)果)
(4)在直角坐標(biāo)系中有點(diǎn)E,和A,C,D構(gòu)成平行四邊形,請(qǐng)直接寫出E點(diǎn)的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,在△ABC中,∠BAC=90°,AB⊥AC,AB=3,BC=5,EF垂直平分BC,點(diǎn)P為直線EF上的任一點(diǎn),則AP+BP的最小值是 . 
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com