
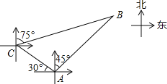
【題目】如圖,甲、乙兩只捕撈船同時在上午![]() 從
從![]() 港出海捕魚.甲船以
港出海捕魚.甲船以![]() 的速度沿西偏北
的速度沿西偏北![]() 方向前進,乙船以
方向前進,乙船以![]() 的速度沿東北方向前進.甲船在
的速度沿東北方向前進.甲船在![]() 航行到達
航行到達![]() 處,此時甲船發現部分漁具丟在乙船上,于是甲船快速(勻速)沿北偏東
處,此時甲船發現部分漁具丟在乙船上,于是甲船快速(勻速)沿北偏東![]() 的方向追趕,結果兩船在
的方向追趕,結果兩船在![]() 處相遇.(其他因素不作考慮)
處相遇.(其他因素不作考慮)
![]() 問乙船在什么時候被甲船追上;
問乙船在什么時候被甲船追上;
![]() 求甲船追趕乙船的速度.
求甲船追趕乙船的速度.
【答案】(1)乙船在![]() 被甲船追上;(2)甲船追趕乙船的速度是每小時(15+15
被甲船追上;(2)甲船追趕乙船的速度是每小時(15+15![]() )千米.
)千米.
【解析】
(1)根據方向角可以得到∠BCA=45°,∠B=30度,過A作AD⊥BC于點D,在直角△ACD中,根據三角函數就可求得AD的長,再在直角△ABD中,根據三角函數即可求得AB的長,就可求得時間;
(2)求出BC的長,根據(1)中的結果求得時間,即可求得速度.
(1)如圖,過A作AD⊥BC于點D.作CG∥AE交AD于點G.
∵乙船沿東北方向前進,∴∠HAB=45°.
∵∠EAC=30°,∴∠CAH=90°﹣30°=60°,∴∠CAB=60°+45°=105°.
∵CG∥EA,∴∠GCA=∠EAC=30°.
∵∠FCD=75°,∴∠BCG=15°,∠BCA=15°+30°=45°,∴∠B=180°﹣∠BCA﹣∠CAB=30°.
在直角△ACD中,∠ACD=45°,AC=2×15![]() 30
30![]() .
.
AD=ACsin45°=30![]() 30.
30.
CD=ACcos45°=30.
在直角△ABD中,∠B=30°,則AB=2AD=60.
則甲船從C處追趕上乙船的時間是:60÷15﹣2=2(小時).
答:乙船在![]() 被甲船追上.
被甲船追上.
(2)BC=CD+BD=30+30![]() .
.
則甲船追趕乙船的速度是每小時(30+30![]() )÷(4-2)=15+15
)÷(4-2)=15+15![]() (千米/時).
(千米/時).
答:甲船追趕乙船的速度是每小時(15+15![]() )千米.
)千米.


科目:初中數學 來源: 題型:
【題目】如圖:CD是⊙O的直徑,線段AB過圓心O,且OA=OB=![]() , CD=2連接AC、AD、BD、BC,AD、CB分別交⊙O于E、F.
, CD=2連接AC、AD、BD、BC,AD、CB分別交⊙O于E、F.
(1)問四邊形CEDF是何種特殊四邊形?請證明你的結論;
(2)當AC與⊙O相切時,四邊形CEDF是正方形嗎?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】教室里的飲水機接通電源就進入自動程序,開機加熱時每分鐘上升10℃,加熱到100℃,停止加熱,水溫開始下降,此時水溫(℃)與開機后用時(min)成反比例關系.直至水溫降至30℃,飲水機關機.飲水機關機后即刻自動開機,重復上述自動程序.若在水溫為30℃時,接通電源后,水溫y(℃)和時間(min)的關系如圖,為了在上午第一節下課時(8:45)能喝到不超過50℃的水,則接通電源的時間可以是當天上午的
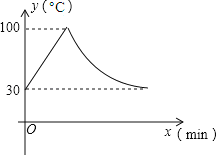
A.7:20 B.7:30 C.7:45 D.7:50
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某汽車銷售公司2月份銷售新上市一種新型低能耗汽車20輛,由于該型汽車的優越的經濟適用性,銷量快速上升,4月份該公司銷售該型汽車達45輛.
(1)求該公司銷售該型汽車3月份和4月份的平均增長率;
(2)該型汽車每輛的進價為10萬元;且銷售a輛汽車,汽車廠返利銷售公司0.03a萬元/輛,該公司的該型車售價為11萬元/輛,若使5月份每輛車盈利不低于2.6萬元,那么該公司5月份至少需要銷售該型汽車多少輛?此時總盈利至少是多少萬元?(盈利=銷售利潤+返利)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了預防疾病,某單位對辦公室采用藥熏消毒法進行消毒,已知藥物燃燒時,室內每立方米空氣中的含藥量y(毫克)與時間x(分鐘)成為正比例,藥物燃燒后,y與x成反比例(如圖),現測得藥物8分鐘燃畢,此時室內空氣中每立方米的含藥量6毫克,請根據題中所提供的信息,解答下列問題:

(1)藥物燃燒時,y關于x的函數關系式為________,自變量x的取值范為________;藥物燃燒后,y關于x的函數關系式為________.
(2)研究表明,當空氣中每立方米的含藥量低于1.6毫克時員工方可進辦公室,那么從消毒開始,至少需要經過________分鐘后,員工才能回到辦公室;
(3)研究表明,當空氣中每立方米的含藥量不低于3毫克且持續時間不低于10分鐘時,才能有效殺滅空氣中的病菌,那么此次消毒是否有效?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四位同學在研究函數y=x2+bx+c(b,c是常數)時,甲發現當x=1時,函數有最小值;乙發現﹣1是方程x2+bx+c=0的一個根;丙發現函數的最小值為3;丁發現當x=2時,y=4,已知這四位同學中只有一位發現的結論是錯誤的,則該同學是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中數學 來源: 題型:
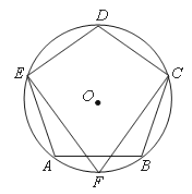
【題目】如圖,☉O是正五邊形ABCDE的外接圓,F是![]() 的中點,連接CF,EF.
的中點,連接CF,EF.
(1)請直接寫出∠CFE= °;
(2)求證:EF=CF;
(3)若☉O的半徑為5,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
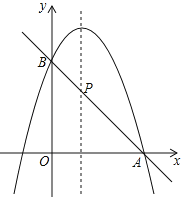
【題目】(10分)已知二次函數![]() .
.
(1)如果二次函數的圖象與x軸有兩個交點,求m的取值范圍;
(2)如圖,二次函數的圖象過點A(3,0),與y軸交于點B,直線AB與這個二次函數圖象的對稱軸交于點P,求點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com