
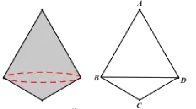
【題目】如圖,某物體由上下兩個圓錐組成,其軸截面![]() 中,
中,![]() ,
,![]() .若下部圓錐的側面積為1,則上部圓錐的側面積為( )
.若下部圓錐的側面積為1,則上部圓錐的側面積為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
先證明△ABD為等邊三角形,得到AB=AD=BD,∠A=∠ABD=∠ADB=60°,由![]() 求出∠CBD=∠CDB=30°,從而求出BC和BD的比值,利用圓錐的側面積的計算方法得到上面圓錐的側面積與下面圓錐的側面積的比等于AB:CB,從而得到上部圓錐的側面積.
求出∠CBD=∠CDB=30°,從而求出BC和BD的比值,利用圓錐的側面積的計算方法得到上面圓錐的側面積與下面圓錐的側面積的比等于AB:CB,從而得到上部圓錐的側面積.
解:∵∠A=60°,AB=AD,
∴△ABD為等邊三角形,
∴AB=AD=BD,∠A=∠ABD=∠ADB=60°,
∵∠ABC=90°,
∴∠CBD=30°,
而CB=CD,
∴△CBD為底角為30°的等腰三角形,
過點C作CE⊥BD于點E,
易得BD=2BE,
∵∠CBD=30°,
∴BE:BC=![]() :2,
:2,
∴BD:BC=![]() :2=
:2=![]() :1,即AB:BC=
:1,即AB:BC=![]() :1,
:1,
∵上面圓錐與下面圓錐的底面相同,
∴上面圓錐的側面積與下面圓錐的側面積的比等于AB:CB,
∴下面圓錐的側面積=![]() .
.
故選:C.



 作業輔導系列答案
作業輔導系列答案科目:初中數學 來源: 題型:
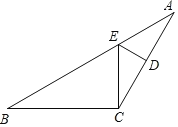
【題目】如圖,在等腰△ABC中,AC=BC,∠ACB=4∠B,點D是AC邊的中點,DE⊥AC,交AB于點E,連接CE.
(1)求∠BCE的度數;
(2)求證:AB=3CE.
查看答案和解析>>
科目:初中數學 來源: 題型:
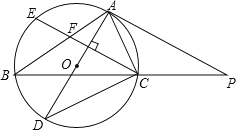
【題目】如圖,AD是△ABC的外接圓⊙O的直徑,點P在BC延長線上,PA是⊙O的切線,且∠B=35°.
(1)求∠PAC的度數.
(2)弦CE⊥AD交AB于點F,若AFAB=12,求AC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“每天鍛煉一小時,健康生活一輩子”,學校準備從小明和小亮2人中隨機選拔一人當“陽光大課間”領操員,體育老師設計的游戲規則是:將四張撲克牌(方塊2、黑桃4、黑桃5、梅花5)的牌面如圖1,撲克牌洗勻后,如圖2背面朝上放置在桌面上.小亮和小明兩人各抽取一張撲克牌,兩張牌面數字之和為奇數時,小亮當選;否則小明當選.
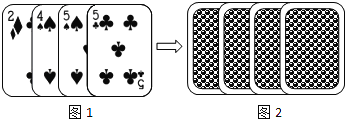
(1)請用樹狀圖或列表法求出所有可能的結果;
(2)請問這個游戲規則公平嗎?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
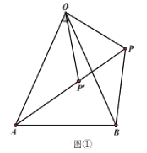
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 外一點,將
外一點,將![]() 繞點
繞點![]() 按順時針方向旋轉
按順時針方向旋轉![]() 得到
得到![]() ,且點
,且點![]() 、
、![]() 、
、![]() 三點在同一直線上.
三點在同一直線上.
(1)(觀察猜想)
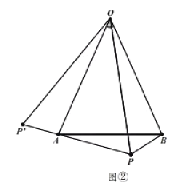
在圖①中,![]() ;在圖②中,
;在圖②中,![]() (用含
(用含![]() 的代數式表示)
的代數式表示)
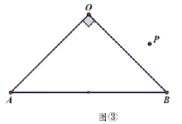
(2)(類比探究)
如圖③,若![]() ,請補全圖形,再過點
,請補全圖形,再過點![]() 作
作![]() 于點
于點![]() ,探究線段
,探究線段![]() ,
,![]() ,
,![]() 之間的數量關系,并證明你的結論;
之間的數量關系,并證明你的結論;
(3)(問題解決)
若![]() ,
,![]() ,
,![]() ,求點
,求點![]() 到
到![]() 的距離.
的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
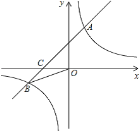
【題目】如圖,已知點![]() ,
,![]() 是一次函數
是一次函數![]() 圖象與反比例函數
圖象與反比例函數![]() 圖象的交點,且一次函數與
圖象的交點,且一次函數與![]() 軸交于
軸交于![]() 點.
點.
(1)求該反比例函數和一次函數的解析式;
(2)連接![]() ,求
,求![]() 的面積;
的面積;
(3)在![]() 軸上有一點
軸上有一點![]() ,使得
,使得![]() ,求出點
,求出點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC繞點A按順時針方向旋轉得到的,連接BE、CF相交于點D.
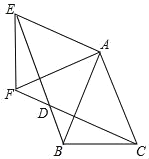
(1)求證:BE=CF;
(2)當四邊形ACDE為菱形時,求BE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com