
【題目】在平面直角坐標系中,對于點![]() 和點
和點![]() 給出如下定義:若
給出如下定義:若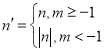 ,則稱點
,則稱點![]() 為點
為點![]() 的絕對點.例如:點
的絕對點.例如:點![]() 的絕對點坐標是
的絕對點坐標是![]() ,點
,點![]() 的絕對點坐標是
的絕對點坐標是![]() .
.
(1)點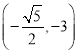 的絕對點坐標是_______.
的絕對點坐標是_______.
(2)若點![]() 在函數
在函數![]()
![]() 的圖像上,其絕對點
的圖像上,其絕對點![]() 的縱坐標
的縱坐標![]() 的取值范圍為
的取值范圍為![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(3)若點![]() 在關于
在關于![]() 的二次函數
的二次函數![]() 圖像上,其絕對點
圖像上,其絕對點![]() 的縱坐標
的縱坐標![]() 的取值范圍是
的取值范圍是![]() 或
或![]() ,其中
,其中![]() ,令
,令![]() ,是否存在
,是否存在![]() 使得
使得![]() 有最大值,若有請求出
有最大值,若有請求出![]() 的最大值及此時
的最大值及此時![]() 的值;若無,請說明理由.
的值;若無,請說明理由.
【答案】(1)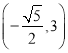 ;(2)3≤k≤5;(3)存在,當t=-
;(2)3≤k≤5;(3)存在,當t=-![]() 時,S取得最大值
時,S取得最大值![]() .
.
【解析】
(1)根據給出的定義可直接得出結果;
(2)根據題意可知y=x-1(-3≤x≤k,k>-3)的圖象上的點P的絕對點Q必在函數![]() 的圖象上,結合圖象即可得到答案;
的圖象上,結合圖象即可得到答案;
(3)首先求出![]() 的頂點坐標,根據題意圖象上的點P的絕對點Q必在函數n′=
的頂點坐標,根據題意圖象上的點P的絕對點Q必在函數n′=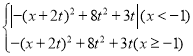 的圖象上,結合-2t與-1的關系確定y的最值,進而用a和b表示出s,根據t的取值范圍求出s的取值范圍.
的圖象上,結合-2t與-1的關系確定y的最值,進而用a和b表示出s,根據t的取值范圍求出s的取值范圍.
解:(1)根據新定義,
∵![]() <-1,∴點
<-1,∴點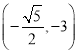 的絕對點坐標是
的絕對點坐標是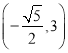 ,
,
故答案為: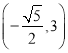 ;
;
(2)依題意,y=x-1(-3≤x≤k,k>-3)圖象上的點P的絕對點Q必在函數n′=![]() 的圖象上(如圖1).
的圖象上(如圖1).
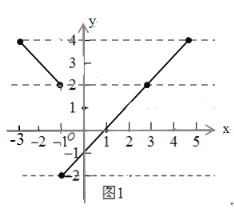
當x=-1時,n′取最小值,n′=-1-1=-2,
當n′=4時,x-1=4或1-x=4,∴x=5或x=-3,
當n′=2時,x-1=2,∴x=3.
∵-2≤n′≤4,
∴由圖象可知,k的取值范圍是:3≤k≤5;
(3)存在.理由如下:
∵y=-x2-4tx+4t2+3t=-(x+2t)2+8t2+3t,∴頂點坐標為(-2t,8t2+3t).
圖象上的點P的絕對點Q必在函數n′=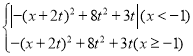 的圖象上.
的圖象上.
Ⅰ.若-2t≥-1,如圖2,
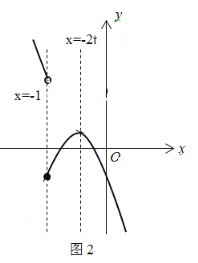
當x<-1時,n′>|-(-1+2t)2+8t2+3t|=|4t2+7t-1|,即a=-4t2-7t+1;
當x≥-1時,n′≤8t2+3t,即b=8t2+3t.
則s=a-b=-12t2-10t+1=-12(t+![]() )2+
)2+![]() ,
,
∴當t=-![]() 時,s取得最大值
時,s取得最大值![]() ;
;
Ⅱ.若-2t<-1,如圖3,
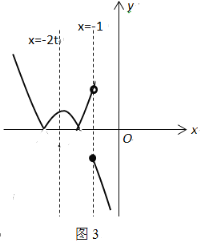
當x<-1時,n′≥0,當x≥-1時,n′≤4t2+7t-1,
與![]() 的取值范圍是
的取值范圍是![]() 或
或![]() 不符,舍去.
不符,舍去.
綜上所述,當t=-![]() 時,s取得最大值
時,s取得最大值![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
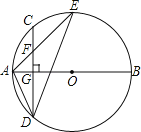
【題目】如圖,AB是⊙O的直徑,弦CD⊥AB于點G,點F是CD上一點,且滿足![]() ,連接AF并延長交⊙O于點E,連接AD、DE,若CF=2,AF=3.給出下列結論:①△ADF∽△AED;②FG=2;③tan∠E=
,連接AF并延長交⊙O于點E,連接AD、DE,若CF=2,AF=3.給出下列結論:①△ADF∽△AED;②FG=2;③tan∠E=![]() ;④S△DEF=4
;④S△DEF=4![]() .
.
其中正確的是 (寫出所有正確結論的序號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,已知二次函數y=ax2+bx+c的圖象與x軸交于A、B兩點,與y軸交于點C對稱軸為直線x=1.直線y=﹣x+c與拋物線y=ax2+bx+c交于C、D兩點,D點在x軸下方且橫坐標小于3,則下列結論:
①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.
其中正確的有( )
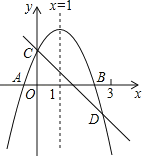
A. 4個 B. 3個 C. 2個 D. 1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法不正確的是( )
A.為了解全市中小學生對網絡直播課的滿意程度,應采用抽樣調查
B.數據![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的方差為
的方差為![]()
C.三角形的的內心到三角形三邊距離相等
D.順次連接對角線垂直的四邊形的中點,所形成的四邊形為菱形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】疫情期間,附中初![]() 級老師們為了解孩子們在家每周體育鍛煉打卡情況,收集部分數據并繪制了如下尚不完整的參與打卡人數與堅持打卡天數的條形統計圖和扇形統計圖:
級老師們為了解孩子們在家每周體育鍛煉打卡情況,收集部分數據并繪制了如下尚不完整的參與打卡人數與堅持打卡天數的條形統計圖和扇形統計圖:
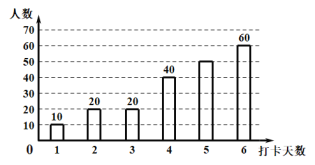
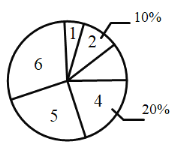
通過分析上面![]() 個統計圖,制作如下表格:
個統計圖,制作如下表格:
統計量 | 平均數 | 中位數 | 眾數 |
天數 | 4.4 | a | b |
(1)填空:![]() _______,
_______,![]() _______,并補全條形統計圖.
_______,并補全條形統計圖.
(2)因為疫情期間,在家體育鍛煉條件受限,所以規定堅持打卡不低于![]() 天即為合格.初
天即為合格.初![]() 級共有學生
級共有學生![]() 人,請你估計初
人,請你估計初![]() 級學生中體育鍛煉合格的人數.
級學生中體育鍛煉合格的人數.
(3)若統計時漏掉![]() 名學生,先將他的打卡天數和原統計的打卡天數合并成一組新數據后,發現平均數增大了,則漏掉的這名學生堅持打卡天數最少是多少天?
名學生,先將他的打卡天數和原統計的打卡天數合并成一組新數據后,發現平均數增大了,則漏掉的這名學生堅持打卡天數最少是多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】受“新冠”疫情的影響,某銷售商在網上銷售![]() 、
、![]() 兩種型號的“手寫板”,獲利頗豐.已知
兩種型號的“手寫板”,獲利頗豐.已知![]() 型,
型,![]() 型手寫板進價、售價和每日銷量如表格所示:
型手寫板進價、售價和每日銷量如表格所示:
進價(元/個) | 售價(元/個) | 銷量(個/日) | |
|
|
|
|
|
|
|
|
根據市場行情,該銷售商對![]() 型手寫板降價銷售,同時對
型手寫板降價銷售,同時對![]() 型手寫板提高售價,此時發現
型手寫板提高售價,此時發現![]() 型手寫板每降低
型手寫板每降低![]() 元就可多賣
元就可多賣![]() 個,
個,![]() 型手寫板每提高
型手寫板每提高![]() 元就少賣
元就少賣![]() 個,要保持每天銷售總量不變,設其中
個,要保持每天銷售總量不變,設其中![]() 型手寫板每天多銷售
型手寫板每天多銷售![]() 個,每天總獲利的利潤為
個,每天總獲利的利潤為![]() 元
元
(1)求![]() 與
與![]() 之間的函數關系式并寫出
之間的函數關系式并寫出![]() 的取值范圍;
的取值范圍;
(2)要使每天的利潤不低于![]() 元,直接寫出
元,直接寫出![]() 的取值范圍;
的取值范圍;
(3)該銷售商決定每銷售一個![]() 型手寫板,就捐
型手寫板,就捐![]() 元給
元給![]() 因“新冠疫情”影響的困難家庭,當
因“新冠疫情”影響的困難家庭,當![]() 時,每天的最大利潤為
時,每天的最大利潤為![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了運送防疫物資,甲、乙兩貨運公司各派出一輛卡車,分別從距目的地240千米和270千米的兩地同時出發,馳援疫區.已知乙公司卡車的平均速度是甲公司卡車的平均速度的1.5倍,甲公司的卡車比乙公司的卡車晚1小時到達目的地,分別求甲、乙兩貨運公司卡車的平均速度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為提升學生的藝術素養,學校計劃開設四門藝術選修課:A.書法;B.繪畫;C.樂器;D.舞蹈.為了解學生對四門功課的喜歡情況,在全校范圍內隨機抽取若干名學生進行問卷調查(每個被調查的學生必須選擇而且只能選擇其中一門).將數據進行整理,并繪制成如下兩幅不完整的統計圖,請結合圖中所給信息解答下列問題:
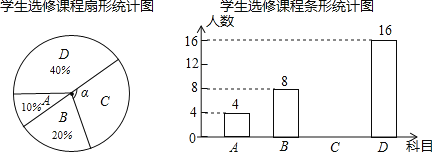
(1)本次調查的學生共有多少人?扇形統計圖中∠α的度數是多少?
(2)請把條形統計圖補充完整;
(3)學校為舉辦2018年度校園文化藝術節,決定從A.書法;B.繪畫;C.樂器;D.舞蹈四項藝術形式中選擇其中兩項組成一個新的節目形式,請用列表法或樹狀圖求出選中書法與樂器組合在一起的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點![]() 是邊長為
是邊長為![]() 的正方形
的正方形![]() 的對角線
的對角線![]() 上的動點,過點
上的動點,過點![]() 分別作
分別作![]() 于點
于點![]()
![]() 于點
于點![]() ,連接
,連接![]() 并延長,交射線
并延長,交射線![]() 于點
于點![]() 交射線
交射線![]() 于點
于點![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() 當
當![]() 點在
點在![]() 上運動時(不包括
上運動時(不包括![]() 兩點),以下結論:①
兩點),以下結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 的最小值是
的最小值是![]() .其中正確的是_______.(把你認為正確結論的序號都填上)
.其中正確的是_______.(把你認為正確結論的序號都填上)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com