
【題目】黃巖島自古以來就是中國的領土,如圖,為維護海洋利益,三沙市一艘海監(jiān)船在黃巖島附近海域巡航,某一時刻海監(jiān)船在A處測得該島上某一目標C在它的北偏東45°方向,海監(jiān)船以30海里每小時的速度沿北偏西30°方向航行2小時后到達B處,此時測得該目標C在它的南偏東75°方向.求:
(1)∠C的度數;
(2)求該船與島上目標C之間的距離 即CB的長度(結果保留根號)
【答案】
(1)
解:由題意得:∠EBA=∠FAB=30°,
∴∠ABC=∠EBC﹣∠EBA=75°﹣30°=45°,
∴∠C=180°﹣45°﹣75°=60°;
(2)
解:過A作AD⊥BC于D,
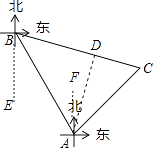
則BD=AD=ABsin∠ABD=2×30× ![]() =30
=30 ![]() ,
,
CD= ![]() =
= ![]() =10
=10 ![]() ,
,
∴CB=BD+CD=(30 ![]() +10
+10 ![]() )(海里),
)(海里),
答:該船與島上目標C之間的距離 即CB的長度為(30 ![]() +10
+10 ![]() )海里.
)海里.
【解析】(1)由由平行線的性質得到∠EBA=∠FAB=30°,進而求得∠ABC,根據三角形的內角和即可求得結論;(2)過A作AD⊥BC于D,根據正弦三角函數和正切三角函數可求得則BD和CD,即可求得結論.
【考點精析】解答此題的關鍵在于理解平行線的性質的相關知識,掌握兩直線平行,同位角相等;兩直線平行,內錯角相等;兩直線平行,同旁內角互補.


科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=﹣x2+2x+3與x軸交于A,B兩點(點A在點B的左邊),與y軸交于點C,連接BC.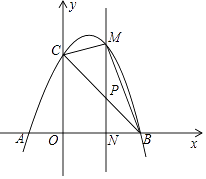
(1)求A,B,C三點的坐標;
(2)若點P為線段BC上一點(不與B,C重合),PM∥y軸,且PM交拋物線于點M,交x軸于點N,當△BCM的面積最大時,求點P的坐標;
(3)在(2)的條件下,當△BCM的面積最大時,在拋物線的對稱軸上存在一點Q,使得△CNQ為直角三角形,求點Q的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著柴靜紀錄片《穹頂之下》的播出,全社會對空氣污染問題越來越重視,空氣凈化器的銷量也大增,商社電器從廠家購進了A,B兩種型號的空氣凈化器,已知一臺A型空氣凈化器的進價比一臺B型空氣凈化器的進價多300元,用7500元購進A型空氣凈化器和用6000元購進B型空氣凈化器的臺數相同.
(1)求一臺A型空氣凈化器和一臺B型空氣凈化器的進價各為多少元?
(2)在銷售過程中,A型空氣凈化器因為凈化能力強,噪音小而更受消費者的歡迎.為了增大B型空氣凈化器的銷量,商社電器決定對B型空氣凈化器進行降價銷售,經市場調查,當B型空氣凈化器的售價為1800元時,每天可賣出4臺,在此基礎上,售價每降低50元,每天將多售出1臺,如果每天商社電器銷售B型空氣凈化器的利潤為3200元,請問商社電器應將B型空氣凈化器的售價定為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,AB=50,AC=30,D、E、F分別是AC、AB、BC的中點.點P從點D出發(fā)沿折線DE﹣EF﹣FC﹣CD以每秒7個單位長的速度勻速運動;點Q從點B出發(fā)沿BA方向以每秒4個單位長的速度勻速運動,過點Q作射線QK⊥AB,交折線BC﹣CA于點G.點P、Q同時出發(fā),當點P繞行一周回到點D時停止運動,點Q也隨之停止.設點P、Q運動的時間是t秒(t>0). 
(1)D、F兩點間的距離是;
(2)射線QK能否把四邊形CDEF分成面積相等的兩部分?若能,求出t的值.若不能,說明理由;
(3)當點P運動到折線EF﹣FC上,且點P又恰好落在射線QK上時,求t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正方形ABCD的邊長為4,點E、F分別在邊AB、ABC上,且AE=BF=1,CE、DF相交于點O,下列結論: ①∠DOC=90°,②OC=OE,③tan∠OCD= ![]() ,④△COD的面積等于四邊形BEOF的面積中,正確的有 ( )
,④△COD的面積等于四邊形BEOF的面積中,正確的有 ( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】以x為自變量的二次函數y=x2﹣2(b﹣2)x+b2﹣1的圖象不經過第三象限,則實數b的取值范圍是( )
A.b≥ ![]()
B.b≥1或b≤﹣1
C.b≥2
D.1≤b≤2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線y=kx+b與拋物線y= ![]() x2交于A(x1 , y1)、B(x2 , y2)兩點,當OA⊥OB時,直線AB恒過一個定點,該定點坐標為 .
x2交于A(x1 , y1)、B(x2 , y2)兩點,當OA⊥OB時,直線AB恒過一個定點,該定點坐標為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一段拋物線:y=﹣x(x﹣2)(0≤x≤2)記為C1 , 它與x軸交于兩點O,A1;將C1繞A1旋轉180°得到C2 , 交x軸于A2;將C2繞A2旋轉180°得到C3 , 交x軸于A3;…如此進行下去,直至得到C6 , 若點P(11,m)在第6段拋物線C6上,則m= . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:
(1)|﹣1|=_____;
(2)﹣(﹣2)=_____;
(3)3+(﹣3)=_____;
(4)3﹣7=_____;
(5)(﹣2)×5=_____;
(6)(﹣9)÷(﹣3)=_____;
(7)(﹣2)3=_____;
(8)![]() =_____.
=_____.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com