
【題目】如圖,在Rt△ABC中,∠C=90°,AB=50,AC=30,D、E、F分別是AC、AB、BC的中點(diǎn).點(diǎn)P從點(diǎn)D出發(fā)沿折線(xiàn)DE﹣EF﹣FC﹣CD以每秒7個(gè)單位長(zhǎng)的速度勻速運(yùn)動(dòng);點(diǎn)Q從點(diǎn)B出發(fā)沿BA方向以每秒4個(gè)單位長(zhǎng)的速度勻速運(yùn)動(dòng),過(guò)點(diǎn)Q作射線(xiàn)QK⊥AB,交折線(xiàn)BC﹣CA于點(diǎn)G.點(diǎn)P、Q同時(shí)出發(fā),當(dāng)點(diǎn)P繞行一周回到點(diǎn)D時(shí)停止運(yùn)動(dòng),點(diǎn)Q也隨之停止.設(shè)點(diǎn)P、Q運(yùn)動(dòng)的時(shí)間是t秒(t>0). 
(1)D、F兩點(diǎn)間的距離是;
(2)射線(xiàn)QK能否把四邊形CDEF分成面積相等的兩部分?若能,求出t的值.若不能,說(shuō)明理由;
(3)當(dāng)點(diǎn)P運(yùn)動(dòng)到折線(xiàn)EF﹣FC上,且點(diǎn)P又恰好落在射線(xiàn)QK上時(shí),求t的值.
【答案】
(1)25
(2)解:射線(xiàn)QK能把四邊形CDEF分成面積相等的兩部分.
如圖,連接DF,過(guò)點(diǎn)F作FH⊥AB于點(diǎn)H,
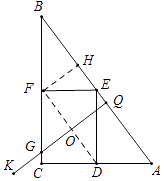
∵D,F(xiàn)是AC,BC的中點(diǎn),
∴DE∥BC,EF∥AC,四邊形CDEF為矩形,
∴QK過(guò)DF的中點(diǎn)O時(shí),即過(guò)矩形CDEF的中點(diǎn),QK把矩形CDEF分為面積相等的兩部分,
此時(shí)QH=OF=12.5.
∵Rt△ABC中,∠C=90°,AB=50,AC=30,
∴BC=40,
由BF=20,△HBF∽△CBA,可得HB=16.
故t= ![]() =
= ![]() =7
=7 ![]() .
.
(3)解:①當(dāng)點(diǎn)P在EF上(2 ![]() ≤t≤5)時(shí),如圖,QB=4t,DE+EP=7t,
≤t≤5)時(shí),如圖,QB=4t,DE+EP=7t,
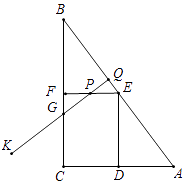
由△PQE∽△BCA,得 ![]() =
= ![]() ,
,
即 ![]() =
= ![]() .
.
∴t=4 ![]() ;
;
②當(dāng)點(diǎn)P在FC上(5≤t≤7 ![]() )時(shí),如圖,已知QB=4t,從而PB=
)時(shí),如圖,已知QB=4t,從而PB= ![]() =
= ![]() =5t,
=5t,
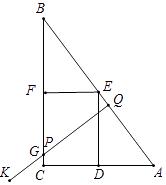
由PF=7t﹣35,BF=20,可得5t=7t﹣35+20.
解得t=7 ![]() .
.
綜上所述,t的值為4 ![]() 或7
或7 ![]() .
.
【解析】解:(1)Rt△ABC中,∠C=90°,AB=50, 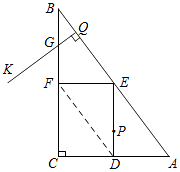
∵D,F(xiàn)是AC,BC的中點(diǎn),
∴DF為△ABC的中位線(xiàn),
∴DF= ![]() AB=25,
AB=25,
即D、F兩點(diǎn)間的距離是25,
所以答案是:25.
【考點(diǎn)精析】關(guān)于本題考查的三角形中位線(xiàn)定理和相似三角形的判定與性質(zhì),需要了解連接三角形兩邊中點(diǎn)的線(xiàn)段叫做三角形的中位線(xiàn);三角形中位線(xiàn)定理:三角形的中位線(xiàn)平行于三角形的第三邊,且等于第三邊的一半;相似三角形的一切對(duì)應(yīng)線(xiàn)段(對(duì)應(yīng)高、對(duì)應(yīng)中線(xiàn)、對(duì)應(yīng)角平分線(xiàn)、外接圓半徑、內(nèi)切圓半徑等)的比等于相似比;相似三角形周長(zhǎng)的比等于相似比;相似三角形面積的比等于相似比的平方才能得出正確答案.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,⊙M與x軸相交于A(2,0)、B(8,0),與y軸相切于點(diǎn)C,P是優(yōu)弧AB上的一點(diǎn),則tan∠APB為( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在△ABC中,AB=AC,∠B=30°,O是BC上一點(diǎn),以點(diǎn)O為圓心,OB長(zhǎng)為半徑作圓,恰好經(jīng)過(guò)點(diǎn)A,并與BC交于點(diǎn)D. 
(1)判斷直線(xiàn)CA與⊙O的位置關(guān)系,并說(shuō)明理由;
(2)若AB= ![]() ,求圖中陰影部分的面積(結(jié)果保留π).
,求圖中陰影部分的面積(結(jié)果保留π).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】定義一個(gè)新的運(yùn)算:a⊕b=  ,則運(yùn)算x⊕2的最小值為( )
,則運(yùn)算x⊕2的最小值為( )
A.﹣3
B.﹣2
C.2
D.3
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】2015年合肥市區(qū)中考理科實(shí)驗(yàn)操作考試備選試題為物理4題(用W1、W2、W3、W4表示)、化學(xué)4題(用H1、H2、H3、H4表示)、生物2題(用S1、S2表示),共10題.某校為備戰(zhàn)實(shí)驗(yàn)操作考試,對(duì)學(xué)生進(jìn)行模擬訓(xùn)練.由學(xué)生在每科測(cè)試時(shí)抽簽選定一個(gè)進(jìn)行實(shí)驗(yàn)操作.若學(xué)生測(cè)試時(shí),第一次抽簽選定物理實(shí)驗(yàn)題,第二次抽簽選定化學(xué)實(shí)驗(yàn)題,第三次抽簽選定生物實(shí)驗(yàn)題.已知王強(qiáng)同學(xué)抽到的物理實(shí)驗(yàn)題為 W1題,
(1)請(qǐng)用樹(shù)形圖法或列表法,表示王強(qiáng)同學(xué)此次抽簽的所有可能情況.
(2)若王強(qiáng)對(duì)化學(xué)的H2、H3y=0.15x和生物的S1實(shí)驗(yàn)準(zhǔn)備得較好,求他能同時(shí)抽到化學(xué)和生物都是準(zhǔn)備較好的實(shí)驗(yàn)題的概率是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,設(shè)點(diǎn)P到原點(diǎn)O的距離為ρ,OP與x軸正方向的交角為a,則用[ρ,a]表示點(diǎn)P的極坐標(biāo),例如:點(diǎn)P的坐標(biāo)為(1,1),則其極坐標(biāo)為[ ![]() ,45°].若點(diǎn)Q的極坐標(biāo)為[4,120°],則點(diǎn)Q的平面坐標(biāo)為( )
,45°].若點(diǎn)Q的極坐標(biāo)為[4,120°],則點(diǎn)Q的平面坐標(biāo)為( ) 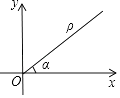
A.(﹣2,﹣2 ![]() )
)
B.(2,﹣2 ![]() )
)
C.(﹣2 ![]() ,﹣2)
,﹣2)
D.(﹣4,﹣4 ![]() )
)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】黃巖島自古以來(lái)就是中國(guó)的領(lǐng)土,如圖,為維護(hù)海洋利益,三沙市一艘海監(jiān)船在黃巖島附近海域巡航,某一時(shí)刻海監(jiān)船在A處測(cè)得該島上某一目標(biāo)C在它的北偏東45°方向,海監(jiān)船以30海里每小時(shí)的速度沿北偏西30°方向航行2小時(shí)后到達(dá)B處,此時(shí)測(cè)得該目標(biāo)C在它的南偏東75°方向.求:
(1)∠C的度數(shù);
(2)求該船與島上目標(biāo)C之間的距離 即CB的長(zhǎng)度(結(jié)果保留根號(hào))
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系xOy中,拋物線(xiàn)y=ax2+bx經(jīng)過(guò)兩點(diǎn)A(﹣1,1),B(2,2).過(guò)點(diǎn)B作BC∥x軸,交拋物線(xiàn)于點(diǎn)C,交y軸于點(diǎn)D.
(1)求此拋物線(xiàn)對(duì)應(yīng)的函數(shù)表達(dá)式及點(diǎn)C的坐標(biāo);
(2)若拋物線(xiàn)上存在點(diǎn)M,使得△BCM的面積為 ![]() ,求出點(diǎn)M的坐標(biāo);
,求出點(diǎn)M的坐標(biāo);
(3)連接OA、OB、OC、AC,在坐標(biāo)平面內(nèi),求使得△AOC與△OBN相似(邊OA與邊OB對(duì)應(yīng))的點(diǎn)N的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】矩形OABC在平面直角坐標(biāo)系中的位置如圖所示,點(diǎn)B的坐標(biāo)為(3,4),D是OA的中點(diǎn),點(diǎn)E在AB上,當(dāng)△CDE的周長(zhǎng)最小時(shí),點(diǎn)E的坐標(biāo)為( ) 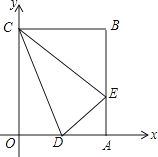
A.(3,1)
B.(3, ![]() )
)
C.(3, ![]() )
)
D.(3,2)
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com