
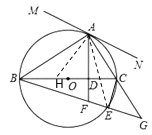
【題目】如圖,![]() 是
是![]() 的直徑,點
的直徑,點![]() 在
在![]() 上,
上,![]() ,垂足為
,垂足為![]() ,
,![]() ,
,![]() 分別交
分別交![]() 延長線于點
延長線于點![]() .
.
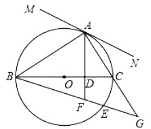
(1)過點![]() 作直線
作直線![]() ,使得
,使得![]() ,判斷直線
,判斷直線![]() 與
與![]() 的位置關系,并說理.
的位置關系,并說理.
(2)若![]() ,
,![]() ,求
,求![]() 的長.
的長.
(3)連接![]() ,探索線段
,探索線段![]() 與
與![]() 間的數量關系,并說明理由.
間的數量關系,并說明理由.
【答案】(1)直線![]() 與
與![]() 相切,理由詳見解析;(2)
相切,理由詳見解析;(2)![]() ;(3)
;(3)![]() ,證明詳見解析.
,證明詳見解析.
【解析】
(1)連接OA,根據![]() 得到
得到![]() ,由BC是
,由BC是![]() 直徑,
直徑,![]() ,得到
,得到![]() ,推出
,推出![]() ,利用
,利用![]() 得到
得到![]() ,推出
,推出![]() ,即可得到直線
,即可得到直線![]() 與
與![]() 相切的結論;
相切的結論;
(2)過點A作AM⊥BG于M,根據![]() 得到∠ACB=∠ABE,證得△AMB∽△BAC,得到
得到∠ACB=∠ABE,證得△AMB∽△BAC,得到![]() ,利用勾股定理求出BC=5,即可求出
,利用勾股定理求出BC=5,即可求出![]() ,再證明△ABM∽△GBA,求出BG=
,再證明△ABM∽△GBA,求出BG=![]() ;
;
(3)在![]() 上截取
上截取![]() ,連接
,連接![]() .證明
.證明![]() ,得到
,得到![]() ,由
,由![]() 得到
得到![]() ,推出
,推出![]() .
.
(1)解:直線![]() 與
與![]() 相切,
相切,
理由:連接OA,
∵![]() ,
,
∴![]() ,
,
∵BC是![]() 直徑,
直徑,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴直線![]() 與
與![]() 相切.
相切.

(2)過點A作AM⊥BG于M,
∵![]() ,
,
∴∠ACB=∠ABE,
∵∠BAC=∠AMB=90°,
∴△AMB∽△BAC,
∴![]() ,
,
∵∠BAC=90°,![]() ,
,![]() ,
,
∴BC=5,
∴![]() ,
,
∴![]() ,
,
∵∠BAC=∠AMB=90°,∠ABM=∠GBA,
∴△ABM∽△GBA,
∴![]() ,
,
∴![]() ,
,
∴BG=![]() ;
;

(3)![]() .
.
理由:在![]() 上截取
上截取![]() ,連接
,連接![]() .
.
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中數學 來源: 題型:
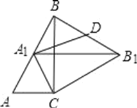
【題目】如圖,Rt△ABC中,∠C=90°,∠ABC=30°,AC=4,△ABC繞點C順時針旋轉得△A1B1C,當A1落在AB邊上時,連接B1B,取BB1的中點D,連接A1D,則A1D的長度是( )
A.![]() B.
B.![]() C.
C.![]() D.6
D.6
查看答案和解析>>
科目:初中數學 來源: 題型:
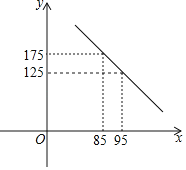
【題目】武漢“新冠肺炎”發生以來,某醫療公司積極復工,加班加點生產醫用防護服,為防控一線助力.以下是該公司以往的市場調查,發現該公司防護服的日銷售量y(套)與銷售單價x(元)之間滿足一次函數關系,如下圖所示,關于日銷售利潤w(元)和銷售單價x(元)的幾組對應值如下表:
銷售單價x(元) | 85 | 95 | 105 |
日銷售利潤w(元) | 875 | 1875 | 1875 |
(注:日銷售利潤=日銷售量×(銷售單價一成本單價))
(1)求y關于x的函數解析式(不要求寫出x的取值范圍);
(2)根據函數圖象和表格所提供的信息,填空:
該公司生產的防護服的成本單價是 元,當銷售單價x= 元時,日銷售利潤w最大,最大值是 元;
(3)該公司復工以后,在政府部門的幫助下,原材料采購成本比以往有了下降,平均起來,每生產一套防護服,成本比以前下降5元.該公司計劃開展科技創新,以降低該產品的成本,如果在今后的銷售中,日銷售量與銷售單價仍存在(1)中的關系.若想實現銷售單價為90元時,日銷售利潤不低于3750元的銷售目標,該產品的成本單價應不超過多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人加工同一種零件,甲每天加工的數量是乙每天加工數量的 1.5 倍,兩人各加工 600 個這種零件,甲比乙少用 5 天.
(1)求甲、乙兩人每天各加工多少個這種零件?
(2)已知甲、乙兩人加工這種零件每天的加工費分別是 150 元和 120 元,現有 3000 個這種零件的加工任務,甲單獨加工一段時間后另有安排,剩余任務由乙單獨完成.如果總加工費不超過 7800 元,那么甲至少加工了多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠A=∠B,AE=BE,點D在AC邊上,∠1=∠2,AE和BD相交于點O.

(1)求證:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
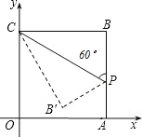
【題目】如圖在平面直角坐標系中,四邊形OABC是正方形,點A的坐標是(4,0),點p為邊AB上的一點,![]() CPB=60°,沿CP折疊正方形后,點B落在平面內B’處,B’的坐標為( )
CPB=60°,沿CP折疊正方形后,點B落在平面內B’處,B’的坐標為( )
A.(2, 2![]() )B.(
)B.(![]() , 2-2
, 2-2![]() )C.(2, 4-2
)C.(2, 4-2![]() )D.(
)D.(![]() , 4-2
, 4-2![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
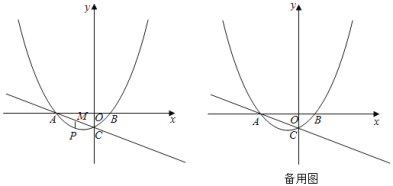
【題目】如圖,拋物線![]() 交x軸于A,B兩點,交y軸于點C.直線
交x軸于A,B兩點,交y軸于點C.直線![]() 經過點A,C.
經過點A,C.
(1)求拋物線的解析式;
(2)點P是拋物線上一動點,過點P作x軸的垂線,交直線AC于點M,設點P的橫坐標為m.
①當![]() 是直角三角形時,求點P的坐標;
是直角三角形時,求點P的坐標;
②作點B關于點C的對稱點![]() ,則平面內存在直線l,使點M,B,
,則平面內存在直線l,使點M,B,![]() 到該直線的距離都相等.當點P在y軸右側的拋物線上,且與點B不重合時,請直接寫出直線
到該直線的距離都相等.當點P在y軸右側的拋物線上,且與點B不重合時,請直接寫出直線![]() 的解析式.(k,b可用含m的式子表示)
的解析式.(k,b可用含m的式子表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
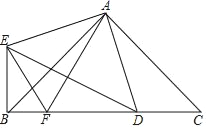
【題目】如圖,△ABC和△ADE分別是以BC,DE為底邊且頂角相等的等腰三角形,點D在線段BC上,AF平分DE交BC于點F,連接BE,EF.
(1)CD與BE相等?若相等,請證明;若不相等,請說明理由;
(2)若∠BAC=90°,求證:BF2+CD2=FD2.
查看答案和解析>>
科目:初中數學 來源: 題型:
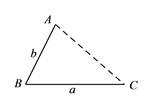
【題目】(1)發現
如圖,點![]() 為線段
為線段![]() 外一動點,且
外一動點,且![]() ,
,![]() .
.
填空:當點![]() 位于____________時,線段
位于____________時,線段![]() 的長取得最大值,且最大值為_________.(用含
的長取得最大值,且最大值為_________.(用含![]() ,
,![]() 的式子表示)
的式子表示)
(2)應用
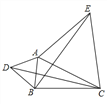
點![]() 為線段
為線段![]() 外一動點,且
外一動點,且![]() ,
,![]() .如圖所示,分別以
.如圖所示,分別以![]() ,
,![]() 為邊,作等邊三角形
為邊,作等邊三角形![]() 和等邊三角形
和等邊三角形![]() ,連接
,連接![]() ,
,![]() .
.
①找出圖中與![]() 相等的線段,并說明理由;
相等的線段,并說明理由;
②直接寫出線段![]() 長的最大值.
長的最大值.
(3)拓展
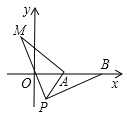
如圖,在平面直角坐標系中,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 為線段
為線段![]() 外一動點,且
外一動點,且![]() ,
,![]() ,
,![]() ,求線段
,求線段![]() 長的最大值及此時點
長的最大值及此時點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com