【題目】如圖，要證明平行四邊形ABCD為正方形，那么我們需要在四邊形ABCD是平行四邊形的基礎上，進一步證明（ ）
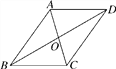
A.AB=AD且AC⊥BDB.AB=AD且AC=BDC.∠A=∠B且AC=BDD.AC和BD互相垂直平分
科目：初中數(shù)學 來源： 題型：
【題目】定義：若兩個函數(shù)y1和y2的自變量x的取值范圍相同，我們不妨把y1和y2的比值y稱為x的比函數(shù)，且比函數(shù)的自變量x的取值范圍不發(fā)生改變．例如：y1＝x2+2x（x＞0），y2＝x（x＞0），則x的比函數(shù)為y＝
＝x+2（x＞0）．
（1）已知y1＝x2﹣4（2≤x≤3），y2＝x+2（2≤x≤3），寫出x的比函數(shù)y的解析式，并求出y的取值范圍；
（2）已知y1＝x+2（x＞1），y2＝x﹣2（x＞1），求x的比函數(shù)y的圖象上的整數(shù)點（橫坐標和縱坐標都為整數(shù)的點）的坐標；
（3）已知y1＝x2﹣x+1，y2＝x2+x+1，若x的比函數(shù)y的圖象與拋物線y3＝x2+2x+k（k為常數(shù)）存在交點，求k的取值范圍．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】已知二次函數(shù)y＝ax（x﹣3）+c（a＜0，0≤x≤3），反比例函數(shù)y＝
（x＞0，k＞0）圖象如圖1所示，反比例函數(shù)y＝（x＞0，k＞0）的圖象經(jīng)過點P（m，n），PM⊥x軸，垂足為M，PN⊥y軸，垂足為N；且OMON＝12．
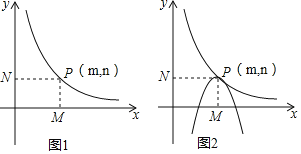
（1）求k的值；
（2）當c＝0時，計算拋物線與x軸的兩個交點之間的距離．
（3）確定二次函數(shù)y＝ax（x﹣3）+c（a＜0，0≤x≤3）對稱軸．
（4）如圖2，當a＝﹣1時，拋物線y＝ax（x﹣3）+c（a＜0；0≤x≤3）有一時刻恰好經(jīng)過P點，且此時拋物線與雙曲線y＝（x＞0，k＞0）有且只有一個公共點P（如圖2所示），我們不妨把此時刻的c記作c1，請直接寫出拋物線y＝ax（x﹣3）+c（a＜0，0≤x≤3）的圖象與雙曲線y＝（x＞0，k＞0）的圖象有一個公共點時c的取值范圍．（溫馨提示：c1作為已知數(shù)，可直接應用哦!）
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】有兩個全等的含30°角的直角三角板重疊在一起，如圖，將△A′B′C′繞AC的中點M轉動，斜邊A′B′剛好過△ABC的直角頂點C，且與△ABC的斜邊AB交于點N，連接AA′、C′C、AC′．若AC的長為2，有以下五個結論：①AA′=1；②C′C⊥A′B′；③點N是邊AB的中點；④四邊形AA′CC′為矩形；⑤A′N=B′C=
，其中正確的有（ ）
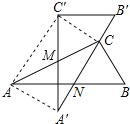
A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】已知關于x的一元二次方程x2﹣（2k+1）x+4k﹣3＝0，
（1）求證：無論k取什么實數(shù)值，該方程總有兩個不相等的實數(shù)根？
（2）當Rt△ABC的斜邊a＝
，且兩條直角邊的長b和c恰好是這個方程的兩個根時，求k的值．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】“校園讀詩詞誦經(jīng)典比賽”結束后，評委劉老師將此次所有參賽選手的比賽成績（得分均為整數(shù)）進行整理，并分別繪制成扇形統(tǒng)計圖和頻數(shù)直方圖，部分信息如下圖：
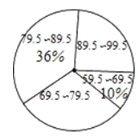
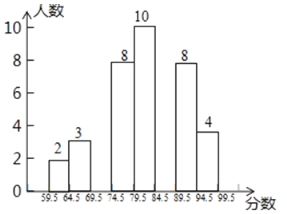
扇形統(tǒng)計圖 頻數(shù)直方圖
（1）參加本次比賽的選手共有________人，參賽選手比賽成績的中位數(shù)在__________分數(shù)段；補全頻數(shù)直方圖.
（2）若此次比賽的前五名成績中有
名男生和
名女生，如果從他們中任選人作為獲獎代表發(fā)言，請利用表格或畫樹狀圖求恰好選中
男女的概率．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】如圖，反比例函數(shù)
的圖象與正比例函數(shù)
的圖象交于點
，且點的橫坐標為2.
（1）求反比例函數(shù)的表達；
（2）若射線
上有點
，
，過點作
與
軸垂直，垂足為點
，交反比例函數(shù)圖象于點
，連接
，
，請求出
的面積.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
