
【題目】如圖,在等邊![]() 中,
中,![]() 分別為
分別為![]() 的中點,延長
的中點,延長![]() 至點
至點![]() ,使
,使![]() ,連結
,連結![]() 和
和![]() .
.
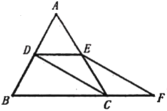
(1)求證:![]()
(2)猜想:![]() 的面積與四邊形
的面積與四邊形![]() 的面積的關系,并說明理由.
的面積的關系,并說明理由.
【答案】(1)見解析;(2)相等,理由見解析.
【解析】
(1)直接利用三角形中位線定理得出DE∥BC,且DE=![]() BC,再利用平行四邊形的判定方法得出答案;
BC,再利用平行四邊形的判定方法得出答案;
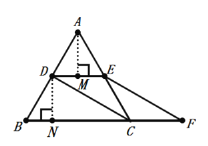
(2)分別過點A,D,作AM⊥DE,DN⊥BC,根據等底等高的三角形面積相等求得S△ADE=S△ECF,再根據S△ADE +S四邊形BDEC=S△ECF +S四邊形BDEC可得出結果.
(1)證明:∵D,E分別為AB,AC的中點,
∴DE是△ABC的中位線,
∴DE∥BC,DE=![]() BC.
BC.
∵CF=![]() BC,
BC,
∴DE∥CF,DE=CF,
∴四邊形DEFC為平行四邊形,
∴CD=EF;
(2)解:相等.理由如下:
分別過點A,D,作AM⊥DE,DN⊥BC,則∠AMD=∠DNB=90°,
∵DE∥BC,
∴∠ADM=∠DBN.
∵AD=DB,
∴△ADM≌△DBN(AAS),
∴AM=DN.
又∵DE=CF,
∴S△ADE=S△ECF (等底等高的三角形面積相等).
∴S△ADE +S四邊形BDEC=S△ECF +S四邊形BDEC,
∴△ABC的面積等于四邊形BDEF的面積.


 應用題作業本系列答案
應用題作業本系列答案科目:初中數學 來源: 題型:
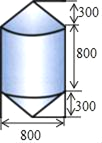
【題目】如圖,錨標浮筒是打撈作業中用來標記錨或沉船位置的,它的上下兩部分是圓柱,中間是一個圓柱(如圖,單位:mm).電鍍時,如果每平方米用鋅0.11kg,要電鍍1000個這樣的錨標浮筒需要用多少鋅?(精確到1kg)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c(a≠0)與x軸交于點A(﹣1,0)和點B,與y軸交于點C,點C關于拋物線對稱軸的對稱點為點D,拋物線頂點為H(1,2).
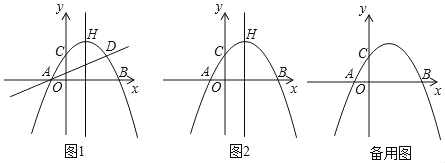
(1)求拋物線的解析式;
(2)點P為直線AD上方拋物線的對稱軸上一動點,連接PA,PD.當S△PAD=3,若在x軸上存在一動點Q,使PQ+![]() QB最小,求此時點Q的坐標及PQ+
QB最小,求此時點Q的坐標及PQ+![]() QB的最小值;
QB的最小值;
(3)若點E為拋物線上的動點,點G,F為平面內的點,以BE為邊構造以B,E,F,G為頂點的正方形,當頂點F或者G恰好落在y軸上時,求點E的橫坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
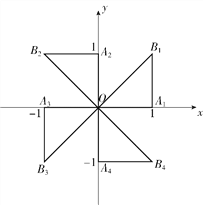
【題目】如圖,在平面直角坐標系xOy中,△OA1B1繞點O逆時針旋轉90°,得△OA2B2;△OA2B2繞點O逆時針旋轉90°,得△OA3B3;△OA3B3繞點O逆時針旋轉90°,得△OA4B4;…;若點A1(1,0),B1(1,1),則點B4的坐標是________,點B 2018的坐標是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司購買了一批![]() 、
、![]() 型芯片,其中
型芯片,其中![]() 型芯片的單價比
型芯片的單價比![]() 型芯片的單價少9元,已知該公司用3120元購買
型芯片的單價少9元,已知該公司用3120元購買![]() 型芯片的條數與用4200元購買
型芯片的條數與用4200元購買![]() 型芯片的條數相等.
型芯片的條數相等.
(1)求該公司購買的![]() 、
、![]() 型芯片的單價各是多少元?
型芯片的單價各是多少元?
(2)若兩種芯片共購買了200條,且購買的總費用為6280元,求購買了多少條![]() 型芯片?
型芯片?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】東海縣是“世界水晶之都”,某水晶產業大戶經銷一種水晶新產品,現準備從國內和國外兩種銷售方案中選擇一種進行銷售,若只在國內銷售,銷售價格y(元/件)與月銷售x(件)的函數關系式為y=﹣![]() x+180,成本為30元/件,無論銷售多少,每月還需支出廣告費6250元,設月利潤為w1(元),若只在國外銷售,銷售價格為180元/件,受各種不確定因素影響,成本為a元/件(a為常數,20≤a≤60),當月銷售量為x(件)時,每月還需繳納
x+180,成本為30元/件,無論銷售多少,每月還需支出廣告費6250元,設月利潤為w1(元),若只在國外銷售,銷售價格為180元/件,受各種不確定因素影響,成本為a元/件(a為常數,20≤a≤60),當月銷售量為x(件)時,每月還需繳納![]() x2元的附加費,設月利潤為w2(元).
x2元的附加費,設月利潤為w2(元).
(1)當x=1000時,y= 元/件,w1= 元.
(2)分別求出w1,w2與x間的函數關系式(不必寫x的取值范圍).
(3)當x為何值時,在國內銷售的月利潤最大?若在國外銷售月利潤的最大值與國內銷售月利潤最大值相同,求a的值.(參考數據:![]() ≈1.4,
≈1.4,![]() ≈1.7,
≈1.7,![]() ≈2.2).
≈2.2).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題背景:如圖![]() ,點
,點![]() 為線段
為線段![]() 外一動點,且
外一動點,且![]() ,若
,若![]() ,
,![]() ,連接
,連接![]() ,求
,求![]() 的最大值.解決方法:以
的最大值.解決方法:以![]() 為邊作等邊
為邊作等邊![]() ,連接
,連接![]() ,推出
,推出![]() ,當點
,當點![]() 在
在![]() 的延長線上時,線段
的延長線上時,線段![]() 取得最大值
取得最大值![]() .
.
問題解決:如圖![]() ,點
,點![]() 為線段
為線段![]() 外一動點,且
外一動點,且![]() ,若
,若![]() ,
,![]() ,連接
,連接![]() ,當
,當![]() 取得最大值時,
取得最大值時,![]() 的度數為_________.
的度數為_________.
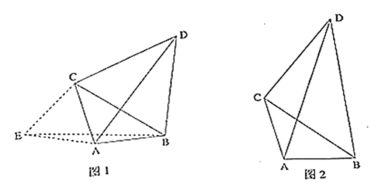
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,E是□ABCD的邊BC延長線上一點,AE交CD于點F,FG∥AD交AB于點G.
(1)填空:圖中與△CEF相似的三角形有__________;(寫出圖中與△CEF相似的所有三角形)
(2)從(1)中選出一個三角形,并證明它與△CEF相似.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程![]()
(1)求證:不論k取什么實數值,這個方程總有實數根;
(2)若等腰三角形ABC的一邊長為![]() ,另兩邊的長b、c恰好是這個方程的兩個根,求△ABC的周長.
,另兩邊的長b、c恰好是這個方程的兩個根,求△ABC的周長.
查看答案和解析>>