【題目】如圖，AB是⊙O的直徑，CD是⊙O的一條弦，且CD⊥AB于點(diǎn)E，CD=4 
，AE=2，則⊙O的半徑為 ． 
【答案】3
【解析】解：∵AB是⊙O的直徑，且CD⊥AB于點(diǎn)E， ∴CE= 
CD= ×4 
=2 ，
在Rt△OCE中，OC2=CE2+OE2 ，
設(shè)⊙O的半徑為r，則OC=r，OE=OA﹣AE=r﹣2，
∴r2=（2 ）2+（r﹣2）2 ，
解得：r=3，
∴⊙O的半徑為3．
所以答案是：3．
【考點(diǎn)精析】關(guān)于本題考查的勾股定理的概念和垂徑定理，需要了解直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2；垂徑定理：平分弦（不是直徑）的直徑垂直于弦，并且平分弦所對(duì)的兩條弧才能得出正確答案．
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：初中數(shù)學(xué) 來(lái)源： 題型：
【題目】如圖，曲線(xiàn)l是由函數(shù)y= 
在第一象限內(nèi)的圖象繞坐標(biāo)原點(diǎn)O逆時(shí)針旋轉(zhuǎn)45°得到的，過(guò)點(diǎn)A（﹣4 
，4 ），B（2 ，2 ）的直線(xiàn)與曲線(xiàn)l相交于點(diǎn)M、N，則△OMN的面積為 ． 
查看答案和解析>>
科目：初中數(shù)學(xué) 來(lái)源： 題型：
【題目】中華文明，源遠(yuǎn)流長(zhǎng)；中華漢字，寓意深廣．為傳承中華優(yōu)秀傳統(tǒng)文化，某校團(tuán)委組織了一次全校3000名學(xué)生參加的“漢字聽(tīng)寫(xiě)”大賽．為了解本次大賽的成績(jī)，校團(tuán)委隨機(jī)抽取了其中200名學(xué)生的成績(jī)作為樣本進(jìn)行統(tǒng)計(jì)，制成如下不完整的統(tǒng)計(jì)圖表：
頻數(shù)頻率分布表
成績(jī)x（分） | 頻數(shù)（人） | 頻率 |
50≤x＜60 | 10 | 0.05 |
60≤x＜70 | 30 | 0.15 |
70≤x＜80 | 40 | n |
80≤x＜90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
根據(jù)所給信息，解答下列問(wèn)題：
（1）m= ， n=；
（2）補(bǔ)全頻數(shù)分布直方圖；
（3）這200名學(xué)生成績(jī)的中位數(shù)會(huì)落在分?jǐn)?shù)段；
（4）若成績(jī)?cè)?0分以上（包括90分）為“優(yōu)”等，請(qǐng)你估計(jì)該校參加本次比賽的3000名學(xué)生中成績(jī)是“優(yōu)”等的約有多少人？
查看答案和解析>>
科目：初中數(shù)學(xué) 來(lái)源： 題型：
【題目】△ABC和△DEF是兩個(gè)全等的等腰直角三角形，∠BAC=∠EDF=90°，△DEF的頂點(diǎn)E與△ABC的斜邊BC的中點(diǎn)重合，將△DEF繞點(diǎn)E旋轉(zhuǎn)，旋轉(zhuǎn)過(guò)程中，線(xiàn)段DE與線(xiàn)段AB相交于點(diǎn)P，線(xiàn)段EF與射線(xiàn)CA相交于點(diǎn)Q． 
（1）如圖①，當(dāng)點(diǎn)Q在線(xiàn)段AC上，且AP=AQ時(shí)，求證：△BPE≌△CQE；
（2）如圖②，當(dāng)點(diǎn)Q在線(xiàn)段CA的延長(zhǎng)線(xiàn)上時(shí)，求證：△BPE∽△CEQ；并求當(dāng)BP=2，CQ=9時(shí)BC的長(zhǎng)．
查看答案和解析>>
科目：初中數(shù)學(xué) 來(lái)源： 題型：
【題目】已知二次函數(shù)y=ax2+bx+c的圖象如圖所示，則下列6個(gè)代數(shù)式：ab、ac、a+b+c、2a+b、2a﹣b中，其值為正的式子的個(gè)數(shù)是（ ）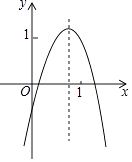 
A.2個(gè)
B.3個(gè)
C.4個(gè)
D.5個(gè)
查看答案和解析>>
科目：初中數(shù)學(xué) 來(lái)源： 題型：
【題目】請(qǐng)用直尺和圓規(guī)在所給的兩個(gè)矩形中各作一個(gè)不為正方形的菱形，且菱形的四個(gè)頂點(diǎn)都在矩形的邊上，面積相同的圖形視為同一種．（保留作圖痕跡）．
查看答案和解析>>
科目：初中數(shù)學(xué) 來(lái)源： 題型：
【題目】已知，如圖，雙曲線(xiàn)y= 
（x＞0）與直線(xiàn)EF交于點(diǎn)A，點(diǎn)B，且AE=AB=BF，連結(jié)AO，BO，它們分別與雙曲線(xiàn)y= 
（x＞0）交于點(diǎn)C，點(diǎn)D，則：
（1）①AB與CD的位置關(guān)系是；
②四邊形ABDC的面積為 ．
查看答案和解析>>
科目：初中數(shù)學(xué) 來(lái)源： 題型：
【題目】如圖，在直角梯形ABCD中，AD∥BC，∠B=90°，AG∥CD交BC于點(diǎn)G，點(diǎn)E、F分別為AG、CD的中點(diǎn)，連接DE、FG． 
（1）求證：四邊形DEGF是平行四邊形；
（2）當(dāng)點(diǎn)G是BC的中點(diǎn)時(shí)，求證：四邊形DEGF是菱形．
查看答案和解析>>
科目：初中數(shù)學(xué) 來(lái)源： 題型：
【題目】如圖四邊形ABCD是菱形，且∠ABC=60，△ABE是等邊三角形，M為對(duì)角線(xiàn)BD（不含B點(diǎn)）上任意一點(diǎn)，將BM繞點(diǎn)B逆時(shí)針旋轉(zhuǎn)60°得到BN，連接EN、AM、CM，則下列五個(gè)結(jié)論中正確的是（ ）
①若菱形ABCD的邊長(zhǎng)為1，則AM+CM的最小值1；
②△AMB≌△ENB；
③S四邊形AMBE=S四邊形ADCM；
④連接AN，則AN⊥BE；
⑤當(dāng)AM+BM+CM的最小值為2 
時(shí)，菱形ABCD的邊長(zhǎng)為2．
A.①②③
B.②④⑤
C.①②⑤
D.②③⑤
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà)：027-86699610 舉報(bào)郵箱：58377363@163.com