
如圖,平面直角坐標系中有一矩形ABCD(O為原點),點A、C分別在x軸、y軸上,且C點坐標為(0,6);將BCD沿BD折疊(D點在OC邊上),使C點落在OA邊的E點上,并將BAE沿BE折疊,恰好使點A落在BD的點F上.
(1)直接寫出∠ABE、∠CBD的度數,并求折痕BD所在直線的函數解析式;
(2)過F點作FG⊥x軸,垂足為G,FG的中點為H,若拋物線![]() 經過B、H、D三點,求拋物線的函數解析式;
經過B、H、D三點,求拋物線的函數解析式;
(3)若點P是矩形內部的點,且點P在(2)中的拋物線上運動(不含B、D點),過點P作PN⊥BC分別交BC和BD于點N、M,設h=PM-MN,試求出h與P點橫坐標x的函數解析式,并畫出該函數的簡圖,分別寫出使PM<NM、PM=MN、PM>MN成立的x的取值范圍。
(1)![]()
(2)![]()
(3)H=MP-MN=![]()
![]()
當0<x<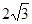 時,h<0,即HP<MN
時,h<0,即HP<MN
當x=![]() 時,h=0,即HP=MN
時,h=0,即HP=MN
當![]() <x<
<x<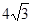 時,h>0,即HP>MN
時,h>0,即HP>MN
解析:解:(1)∠ABE=∠CBD=30°
在△ABE中,AB=6
BC=BE=![]()
CD=BCtan30°=4
∴OD=OC-CD=2
∴B(![]() ,6) D(0,2)
,6) D(0,2)
設BD所在直線的函數解析式是y=kx+b
![]()
![]()
![]() ∴
∴ 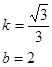
所以BD所在直線的函數解析式是![]()
(2)∵EF=EA=ABtan30°=![]() ∠FEG=180°-∠FEB-∠AEB=60°
∠FEG=180°-∠FEB-∠AEB=60°
又∵FG⊥OA
∴FG=EFsin60°=3 GE=EFcos60°=![]() OG=OA-AE-GE=
OG=OA-AE-GE=![]()
又H為FG中點
∴H(![]() ,
,![]() ) …………4分
) …………4分
∵B(![]() ,6) 、 D(0,2)、 H(
,6) 、 D(0,2)、 H(![]() ,
,![]() )在拋物線
)在拋物線![]() 圖象上
圖象上
![]()
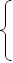
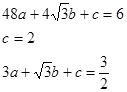 ∴
∴ 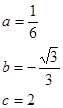
∴拋物線的解析式是![]()
(3)∵MP=![]()
MN=6-![]()
H=MP-MN=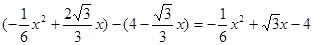
由![]() 得
得![]()
該函數簡圖如圖所示:
當0<x<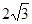 時,h<0,即HP<MN
時,h<0,即HP<MN
當x=![]() 時,h=0,即HP=MN
時,h=0,即HP=MN
當![]() <x<
<x<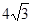 時,h>0,即HP>MN
時,h>0,即HP>MN


科目:初中數學 來源: 題型:
 =2
=2| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
| a+2 |
| S△CAD |
| S△DGH |
| AD |
| GH |
| FC+2AE |
| 3AM |

查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖在平面直角坐標系中,A點坐標為(8,0),B點坐標為(0,6)C是線段AB的中點.請問在y軸上是否存在一點P,使得以P、B、C為頂點的三角形與△AOB相似?若存在,求出P點坐標;若不存在,說明理由.
如圖在平面直角坐標系中,A點坐標為(8,0),B點坐標為(0,6)C是線段AB的中點.請問在y軸上是否存在一點P,使得以P、B、C為頂點的三角形與△AOB相似?若存在,求出P點坐標;若不存在,說明理由.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com