
【題目】幾何證明:
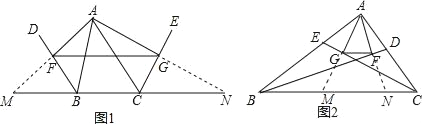
(1)已知:如圖1,BD、CE分別是△ABC的外角平分線,過點A作AF⊥BD,AG⊥CE,垂足分別是F、G,連接FG,延長AF、AG,與直線BC相交.求證:FG=![]() (AB+BC+AC).
(AB+BC+AC).
(2)若BD、CE分別是△ABC的內角平分線,其余條件不變(如圖1),線段FG與△ABC的三邊又有怎樣的數量關系?寫出你的猜想,并給予證明.
【答案】(1)見解析;(2)線段FG與△ABC三邊的數量關系是FG=![]() (AB+AC﹣BC),理由見解析
(AB+AC﹣BC),理由見解析
【解析】
(1)利用全等三角形的判定定理ASA證得△ABF≌△MBF,然后由全等三角形的對應邊相等進一步推出MB=AB,AF=MF,同理CN=AC,AG=NG,由此可以證明FG為△AMN的中位線,然后利用中位線定理求得FG=![]() (AB+BC+AC);(2)延長AF、AG,與直線BC相交于M、N,與(1)類似可以證出答案.
(AB+BC+AC);(2)延長AF、AG,與直線BC相交于M、N,與(1)類似可以證出答案.
(1)如圖1,∵AF⊥BD,∠ABF=∠MBF,
∴∠BAF=∠BMF,
在△ABF和△MBF中,
∵ ,
,
∴△ABF≌△MBF(ASA)
∴MB=AB
∴AF=MF,
同理:CN=AC,AG=NG,
∴FG是△AMN的中位線
∴FG=![]() MN,
MN,
=![]() (MB+BC+CN),
(MB+BC+CN),
=![]() (AB+BC+AC).
(AB+BC+AC).
(2)圖2中,FG=![]() (AB+AC﹣BC)
(AB+AC﹣BC)
理由如下:如圖2,
延長AG、AF,與直線BC相交于M、N,
∵由(1)中證明過程類似證△ABF≌△NBF,
∴NB=AB,AF=NF,
同理CM=AC,AG=MG
∴FG=![]() MN,
MN,
∴MN=2FG,
∴BC=BN+CM﹣MN=AB+AC﹣2FG,
∴FG=![]() (AB+AC﹣BC),
(AB+AC﹣BC),
答:線段FG與△ABC三邊的數量關系是FG=![]() (AB+AC﹣BC).
(AB+AC﹣BC).


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】甲乙兩件服裝的進價共500元,商場決定將甲服裝按30%的利潤定價,乙服裝按20%的利潤定價,實際出售時,兩件服裝均按9折出售,商場賣出這兩件服裝共獲利67元.
(1)求甲乙兩件服裝的進價各是多少元;
(2)由于乙服裝暢銷,制衣廠經過兩次上調價格后,使乙服裝每件的進價達到242元,求每件乙服裝進價的平均增長率;
(3)若每件乙服裝進價按平均增長率再次上調,商場仍按9折出售,定價至少為多少元時,乙服裝才可獲得利潤(定價取整數).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了更好治理西太湖水質,保護環境,市治污公司決定購買10 臺污水處理設備,現有A、B兩種型號的設備,其中每臺的價格,月處理污水量如下表:

經調查:購買-臺A型設備比購買一-臺B型設備多2萬元,購買2臺A型設備比購買4臺B型設備少4萬元.
(1)求a、b的值;
(2)經預算:市治污公司購買污水處理設備的資金不超過47萬元,并且該月要求處理西太湖的污水量不低于1860 噸,則有哪幾種購買方案?請指出最省錢的一種購買方案,并指出相應的費用.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,O為直線AB上一點,過點O作射線OC,![]() ,將一直角三角板
,將一直角三角板![]() 的直角頂點放在點O處,一邊ON在射線OA上,另一邊OM與OC都在直線AB的上方.
的直角頂點放在點O處,一邊ON在射線OA上,另一邊OM與OC都在直線AB的上方.
![]() 將圖1中的三角板繞點O以每秒
將圖1中的三角板繞點O以每秒![]() 的速度沿逆時針方向旋轉一周
的速度沿逆時針方向旋轉一周![]() 如圖2,經過t秒后,ON落在OC邊上,則
如圖2,經過t秒后,ON落在OC邊上,則![]() ______秒
______秒![]() 直接寫結果
直接寫結果![]() .
.
![]() 如圖2,三角板繼續繞點O以每秒
如圖2,三角板繼續繞點O以每秒![]() 的速度沿逆時針方向旋轉到起點OA上
的速度沿逆時針方向旋轉到起點OA上![]() 同時射線OC也繞O點以每秒
同時射線OC也繞O點以每秒![]() 的速度沿逆時針方向旋轉一周,
的速度沿逆時針方向旋轉一周,
![]() 當OC轉動9秒時,求
當OC轉動9秒時,求![]() 的度數.
的度數.
![]() 運動多少秒時,
運動多少秒時,![]() ?請說明理由.
?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=kx+b與反比例函數 ![]() 的圖象交于A(m,6),B(3,n)兩點.
的圖象交于A(m,6),B(3,n)兩點. 
(1)求一次函數的解析式;
(2)根據圖象直接寫出 ![]() 的x的取值范圍;
的x的取值范圍;
(3)求△AOB的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學活動課上,某學習小組對有一內角為120°的平行四邊形ABCD(∠BAD=120°)進行探究:將一塊含60°的直角三角板如圖放置在平行四邊形ABCD所在平面內旋轉,且60°角的頂點始終與點C重合,較短的直角邊和斜邊所在的兩直線分別交線段AB,AD于點E,F(不包括線段的端點).
(1)初步嘗試
如圖1,若AD=AB,求證:①△BCE≌△ACF,②AE+AF=AC;
(2)類比發現
如圖2,若AD=2AB,過點C作CH⊥AD于點H,求證:AE=2FH;
(3)深入探究
如圖3,若AD=3AB,探究得: ![]() 的值為常數t,則t= .
的值為常數t,則t= . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】菱形ABCD中,兩條對角線AC,BD相交于點O,∠MON+∠BCD=180°,∠MON繞點O旋轉,射線OM交邊BC于點E,射線ON交邊DC于點F,連接EF.
(1)如圖1,當∠ABC=90°時,△OEF的形狀是;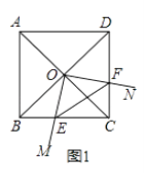
(2)如圖2,當∠ABC=60°時,請判斷△OEF的形狀,并說明理由;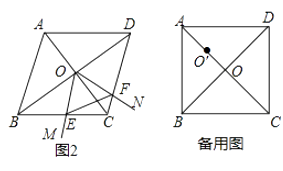
(3)在(1)的條件下,將∠MON的頂點移到AO的中點O′處,∠MO′N繞點O′旋轉,仍滿足∠MO′N+∠BCD=180°,射線O′M交直線BC于點E,射線O′N交直線CD于點F,當BC=4,且 ![]() =
= ![]() 時,直接寫出線段CE的長.
時,直接寫出線段CE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,甲乙兩人在游泳池A處發現游泳池中的P處有人求救,甲立即跳入池中去救人,速度為1米/秒,乙以3.5米/秒的速度沿游泳池邊跑到距A不遠處的B處,撿起一個游泳圈再跳入池中去救人,甲游了20秒到達P處,兩秒后乙到達P處.若∠PAB與∠PBC互余,且cos∠PBC= ![]() ,求乙的游泳速度.
,求乙的游泳速度. 
查看答案和解析>>
科目:初中數學 來源: 題型:
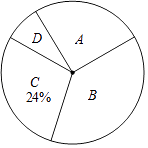
【題目】近期電視劇《人民的名義》熱播,某校“話劇表演”社團在本校學生中開展學生知曉情況專題調查活動,采取隨機抽樣的方式進行問卷調查,問卷調查的結果分為A,B,C,D四類.其中,A類表示“自己看過”,B類表示“聽家長講過”,
C類表示“聽同學講過”,D類表示“不知道”,劃分類別后的數據整理如表:
類別 | A | B | C | D |
頻數 | 30 | 40 | 24 | b |
頻率 | a | 0.4 | 0.24 | 0.06 |
(1)表中的a=b=;
(2)根據表中數據,求扇形統計圖中類別為B的學生數所對應的扇形圓心角的度數;
(3)若該校有學生1000名,根據調查結果估計該校學生中類別為C的人數約為多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com