
【題目】已知,拋物線y=ax+bx+4與x軸交于點A(-3,0)和B(2,0),與y軸交于點C.
(1)求拋物線的解析式;
(2)如圖1,若點D為CB的中點,將線段DB繞點D旋轉,點B的對應點為點G,當點G恰好落在拋物線的對稱軸上時,求點G的坐標;
(3)如圖2,若點D為直線BC或直線AC上的一點,E為x軸上一動點,拋物線![]() 對稱軸上是否存在點F,使以B,D,F,E為頂點的四邊形為菱形?若存在,請求出點F的坐標;若不存在,請說明理由.
對稱軸上是否存在點F,使以B,D,F,E為頂點的四邊形為菱形?若存在,請求出點F的坐標;若不存在,請說明理由.
【答案】
(1)
由A(-3,0)和B(2,0),得: ![]()
即 ![]() = ax+bx+4
= ax+bx+4
∴ ![]()
∴ ![]()
∴ ![]() .
.
(2)
易得C(0,4),則BC= ![]() .
.
由 ![]() 可對稱軸為x=
可對稱軸為x= 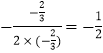 ,
,
則可設點G的坐標為 ![]() ,
,
∵點D是BC的中點
∴點D的坐標為 ![]() ,
, ![]()
由旋轉可得,DG=DB
∴ ![]() ……………
……………
∴ ![]() ………
………
∴點G的坐標為 ![]() 或
或 ![]()
(3)
①當BE為對角線時,因為菱形的對角線互相垂直平分,所以此時D即為對稱軸與AC的交點或對稱軸對BC的交點,F為點D關于x軸的對稱點,
設 ![]() ,
,
∵C ![]() ,A
,A ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴當 ![]() 時,
時, ![]() ,
,
∴D ![]() ,
,
∴F ![]() ;
;
易得 ![]()
∴當 ![]() 時,y=5,
時,y=5,
∴D ![]() ,
,
∴F ![]() ;
;
②當BE為菱形的邊時,有DF∥BE
I)當點D在直線BC上時
![]()
設D ![]() ,則點F
,則點F ![]()
∵四邊形BDFE是菱形
∴FD=DB
根據勾股定理得, ![]()
整理得: ![]() =0,
=0,
解得: ![]() ,
, ![]()
∴F ![]() 或
或 ![]()
II)當點D在直線AC上時
設D ![]() ,則點F
,則點F ![]()
∵四邊形BFDE是菱形,
∴FD=FB,
根據勾股定理得, ![]()
整理得: ![]() ,
,
解得: ![]() (舍去),
(舍去), ![]()
∴F ![]() ,
,
綜上所述,點F的坐標分別為: ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
【解析】(1)可將三個點的分別代入拋物線可解出;或都運用兩點式簡便求解;(2)由旋轉可得DG=DB,因為D是BC中點,所以DB= ![]() BC,求DB的長,和D的坐標,因為G在對稱軸上的點,則橫坐標為
BC,求DB的長,和D的坐標,因為G在對稱軸上的點,則橫坐標為 ![]() ,由勾股定理構造方程,解出G的縱坐標;(3)分類討論:BE在x軸上,所以當BE為對角線上時,則FD也為對角線,它們互相平分且垂直,而點F在對稱軸上,D也在對稱軸上,所以點D與F關于x軸對稱,則點D為AC與對稱軸的交點,BC與對稱軸的交點,求出點D即可;當BE為邊時,根據對邊平行可得必有DF//BE,則D,F的縱坐標相等,則當點D在BC上時,可設點D的坐標,從而可得點F的坐標由FD=DB,構造方程解得D的坐標,F的坐標;當點D在AC上時,同理.
,由勾股定理構造方程,解出G的縱坐標;(3)分類討論:BE在x軸上,所以當BE為對角線上時,則FD也為對角線,它們互相平分且垂直,而點F在對稱軸上,D也在對稱軸上,所以點D與F關于x軸對稱,則點D為AC與對稱軸的交點,BC與對稱軸的交點,求出點D即可;當BE為邊時,根據對邊平行可得必有DF//BE,則D,F的縱坐標相等,則當點D在BC上時,可設點D的坐標,從而可得點F的坐標由FD=DB,構造方程解得D的坐標,F的坐標;當點D在AC上時,同理.
【考點精析】解答此題的關鍵在于理解二次函數的圖象的相關知識,掌握二次函數圖像關鍵點:1、開口方向2、對稱軸 3、頂點 4、與x軸交點 5、與y軸交點,以及對二次函數的性質的理解,了解增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖是二次函數y=ax2+bx+c圖象的一部分,且過點A (3,0),二次函數圖象的對稱軸是x=1.下列結論:①b2>4ac;②ac>0; ③a﹣b+c>0; ④4a+2b+c<0.其中錯誤的結論有( ) 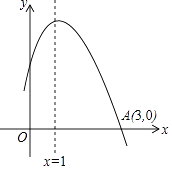
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,拋物線y=ax2+ ![]() +c經過原點O和A(4,2),與x軸交于點C,點M、N同時從原點O出發,點M以2個單位/秒的速度沿y軸正方向運動,點N以1個單位/秒的速度沿x軸正方向運動,當其中一個點停止運動時,另一點也隨之停止.
+c經過原點O和A(4,2),與x軸交于點C,點M、N同時從原點O出發,點M以2個單位/秒的速度沿y軸正方向運動,點N以1個單位/秒的速度沿x軸正方向運動,當其中一個點停止運動時,另一點也隨之停止.
(1)求拋物線的解析式和點C的坐標;
(2)在點M、N運動過程中,
①若線段MN與OA交于點G,試判斷MN與OA的位置關系,并說明理由;
②若線段MN與拋物線相交于點P,探索:是否存在某一時刻t,使得以O、P、A、C為頂點的四邊形是等腰梯形?若存在,請求出t值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2013年9月23日強臺風“天兔”登錄深圳,伴隨著就是狂風暴雨梧桐山山坡上有一棵與水平面垂直的大樹,臺風過后,大樹被刮傾斜后折斷倒在山坡上,樹的頂部恰好接觸到坡面(如圖所示).已知山坡的坡角∠AEF=23°,量得樹干的傾斜角為∠BAC=38°,大樹被折斷部分和坡面所成的角∠ADC=60°,AD=3m.

(1)求∠DAC的度數;
(2)求這棵大樹折斷前的高度?(結果保留根號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在□ABCD中,對角線AC與BD相交于點O,過點O作一條直線分別交AB,CD于點E,F.
(1)求證:OE=OF;
(2)若AB=6,BC=5,OE=2,求四邊形BCFE的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是一輛小汽車與墻平行停放的平面示意圖,汽車靠墻一側與墻MN平行且距離為0.8米,已知小汽車車門寬AO為1.2米,當車門打開角度∠AOB為40°時,車門是否會碰到墻?請說明理由。(參考數據:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題背景
如圖1,在正方形ABCD的內部,作∠DAE=∠ABF=∠BCG=∠CDH,根據三角形全等的條件,易得△DAE≌△ABF≌△BCG≌△CDH,從而得到四邊形EFGH是正方形。
類比研究
如圖2,在正△ABC的內部,作∠BAD=∠CBE=∠ACF,AD,BE,CF兩兩相交于D,E,F三點(D,E,F三點不重合)。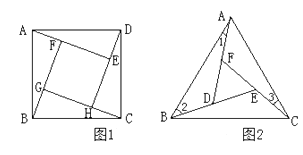
(1)△ABD,△BCE,△CAF是否全等?如果是,請選擇其中一對進行證明;
(2)△DEF是否為正三角形?請說明理由;
(3)進一步探究發現,△ABD的三邊存在一定的等量關系,設 ![]() ,
, ![]() ,
, ![]() ,請探索
,請探索 ![]() ,
, ![]() ,
, ![]() 滿足的等量關系。
滿足的等量關系。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線y=﹣x+3與x軸、y軸分別交于A,B兩點,拋物線y=﹣x2+bx+c經過A,B兩點,點P在線段OA上,從點O出發,向點A以1個單位/秒的速度勻速運動;同時,點Q在線段AB上,從點A出發,向點B以 ![]() 個單位/秒的速度勻速運動,連接PQ,設運動時間為t秒.
個單位/秒的速度勻速運動,連接PQ,設運動時間為t秒.
(1)求拋物線的解析式;
(2)當t為何值時,△APQ為直角三角形;
(3)過點P作PE∥y軸,交AB于點E,過點Q作QF∥y軸,交拋物線于點F,連接EF,當EF∥PQ時,求點F的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校在踐行“社會主義核心價值觀”演講比賽中,對名列前20名的選手的綜合分數m進行分組統計,結果如表所示:
組號 | 分組 | 頻數 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |

(1)求a的值;
(2)若用扇形圖來描述,求分數在8≤m<9內所對應的扇形圖的圓心角大小;
(3)將在第一組內的兩名選手記為:A1、A2 , 在第四組內的兩名選手記為:B1、B2 , 從第一組和第四組中隨機選取2名選手進行調研座談,求第一組至少有1名選手被選中的概率(用樹狀圖或列表法列出所有可能結果).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com