
【題目】在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 邊上的中點,動點
邊上的中點,動點![]() 在邊
在邊![]() 上,連接
上,連接![]() ,過點
,過點![]() 作
作![]() 分別交射線
分別交射線![]() 、射線
、射線![]() 于點
于點![]() 、
、![]() .
.

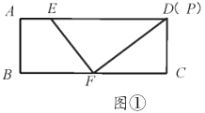
(1)如圖1,當(dāng)點![]() 與點
與點![]() 重合時,求
重合時,求![]() 的長;
的長;
(2)如圖2,當(dāng)點![]() 在線段
在線段![]() 上(不與
上(不與![]() ,
,![]() 重合)且
重合)且![]() 時,求
時,求![]() 的長;
的長;
(3)線段![]() 將矩形分成兩個部分,設(shè)較小部分的面積為
將矩形分成兩個部分,設(shè)較小部分的面積為![]() ,
,![]() 長為
長為![]() ,求
,求![]() 與
與![]() 的函數(shù)關(guān)系式.
的函數(shù)關(guān)系式.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;![]()
【解析】
(1)利用勾股定理即可求得答案;
(2)利用![]() 和
和![]() ,對應(yīng)邊成比例,結(jié)合
,對應(yīng)邊成比例,結(jié)合![]() ,即可求得答案;
,即可求得答案;
(3)分類討論,當(dāng)![]() 在線段
在線段![]() 上時和
上時和![]() 在線段
在線段![]() 的延長線上時,根據(jù)(2)的方法,利用相似三角形對應(yīng)邊成比例結(jié)合三角形面積公式即可求得答案.
的延長線上時,根據(jù)(2)的方法,利用相似三角形對應(yīng)邊成比例結(jié)合三角形面積公式即可求得答案.
(1)如圖①,當(dāng)![]() 、
、![]() 重合時,
重合時,![]() ,
,
∵![]() 為
為![]() 中點,
中點,
∴![]() ,
,
在矩形![]() 中,
中,![]() ,
,![]() ,
,
![]() ;
;
(2)如圖②,過![]() 作
作![]() 于
于![]() ,則
,則![]() ,
,
在矩形ABCD中,![]() ,又
,又![]() ,則
,則![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() ;
;

(3)如圖②當(dāng)![]() 在線段
在線段![]() 上時,過
上時,過![]() 作
作![]() 于
于![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 即
即![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
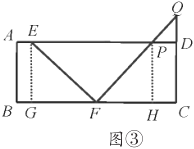
如圖③,當(dāng)![]() 在線段
在線段![]() 的延長線上時,
的延長線上時,
過![]() 作
作![]() 于
于![]() ,過
,過![]() 作
作![]() 于
于![]() ,則
,則![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 即
即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,


科目:初中數(shù)學(xué) 來源: 題型:
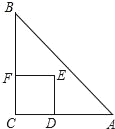
【題目】如圖,Rt△ABC中,AC=BC=2,正方形CDEF的頂點D、F分別在AC、BC邊上,設(shè)CD的長度為x,△ABC與正方形CDEF重疊部分的面積為y,則下列圖象中能表示y與x之間的函數(shù)關(guān)系的是( )
A. 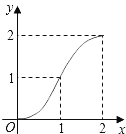 B.
B. 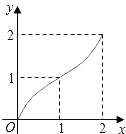
C. 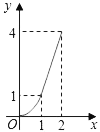 D.
D. 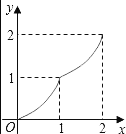
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平行四邊形![]() 中,
中,![]() 的平分線交
的平分線交![]() 于點E,交
于點E,交![]() 的延長線于F,以
的延長線于F,以![]() 為鄰邊作平行四邊形
為鄰邊作平行四邊形![]() 。
。
(1)證明平行四邊形![]() 是菱形;
是菱形;
(2)若![]() ,連結(jié)
,連結(jié)![]() ,①求證:
,①求證:![]() ;②求
;②求![]() 的度數(shù);
的度數(shù);
(3)若![]() ,
,![]() ,
,![]() ,M是
,M是![]() 的中點,求
的中點,求![]() 的長。
的長。

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在邊長為1個單位長度的小正方形網(wǎng)格中,![]() 的頂點均在格點上,在建立平面直角坐標(biāo)系后,點
的頂點均在格點上,在建立平面直角坐標(biāo)系后,點![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
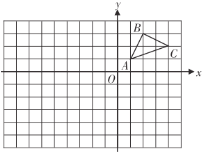
(1)將![]() 向左平移3個單位得到
向左平移3個單位得到![]() ,畫出
,畫出![]() ;
;
(2)在第三象限內(nèi),以![]() 為位似中心,將
為位似中心,將![]() 放大到原大的2倍,畫出放大后對應(yīng)的
放大到原大的2倍,畫出放大后對應(yīng)的![]() ;
;
(3)寫出![]() 的坐標(biāo)______,
的坐標(biāo)______,![]() 的坐標(biāo)______.
的坐標(biāo)______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
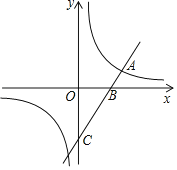
【題目】在平面直角坐標(biāo)系xOy中,直線y=2x﹣6與雙曲線![]() (k≠0)的一個交點為A(m,2),與x軸交于點B,與y軸交于點C.
(k≠0)的一個交點為A(m,2),與x軸交于點B,與y軸交于點C.
(1)求點B的坐標(biāo)及k的值;
(2)若點P在x軸上,且△APC的面積為16,求點P的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知正方形ABCD中,BE平分∠DBC且交CD邊于點E,將△BCE繞點C順時針旋轉(zhuǎn)到△DCF的位置,并延長BE交DF于點G.
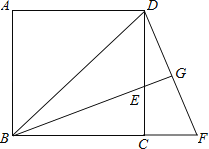
(1)求證:△BDG∽△DEG;
(2)若EGBG=4,求BE的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
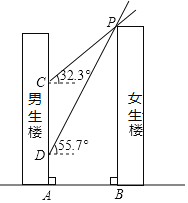
【題目】如圖,男生樓在女生樓的左側(cè),兩樓高度均為90m,樓間距為AB,冬至日正午,太陽光線與水平面所成的角為![]() ,女生樓在男生樓墻面上的影高為CA;春分日正午,太陽光線與水平面所成的角為
,女生樓在男生樓墻面上的影高為CA;春分日正午,太陽光線與水平面所成的角為![]() ,女生樓在男生樓墻面上的影高為DA,已知
,女生樓在男生樓墻面上的影高為DA,已知![]() .
.
![]() 求樓間距AB;
求樓間距AB;
![]() 若男生樓共30層,層高均為3m,請通過計算說明多少層以下會受到擋光的影響?
若男生樓共30層,層高均為3m,請通過計算說明多少層以下會受到擋光的影響?![]() 參考數(shù)據(jù):
參考數(shù)據(jù):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com