
【題目】如圖![]() ,二次函數
,二次函數![]() 的圖象與一次函數
的圖象與一次函數![]() 的圖象交于
的圖象交于![]() ,
, ![]() 兩點,點
兩點,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 在第一象限內,點
在第一象限內,點![]() 是二次函數圖象的頂點,點
是二次函數圖象的頂點,點![]() 是一次函數
是一次函數![]() 的圖象與
的圖象與![]() 軸的交點,過點
軸的交點,過點![]() 作
作![]() 軸的垂線,垂足為
軸的垂線,垂足為![]() ,且
,且![]() .
.
(![]() )求直線
)求直線![]() 和直線
和直線![]() 的解析式.
的解析式.
(2)點![]() 是線段
是線段![]() 上一點,點
上一點,點![]() 是線段
是線段![]() 上一點,
上一點, ![]() 軸,射線
軸,射線![]() 與拋物線交于點
與拋物線交于點![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() ,
, ![]() 于點
于點![]() ,當
,當![]() 與
與![]() 的乘積最大時,在線段
的乘積最大時,在線段![]() 上找一點
上找一點![]() (不與點
(不與點![]() ,點
,點![]() 重合),使
重合),使![]() 的值最小,求點
的值最小,求點![]() 的坐標和
的坐標和![]() 的最小值.
的最小值.
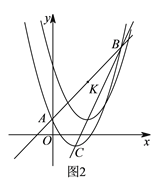
(![]() )如圖
)如圖![]() ,直線
,直線![]() 上有一點
上有一點![]() ,將二次函數
,將二次函數![]() 沿直線
沿直線![]() 平移,平移的距離是
平移,平移的距離是![]() ,平移后拋物線使點
,平移后拋物線使點![]() ,點
,點![]() 的對應點分別為點
的對應點分別為點![]() ,點
,點![]() ;當
;當![]() 是直角三角形時,求t的值.
是直角三角形時,求t的值.
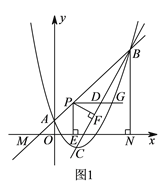
【答案】(1)![]() ,
, ![]() ;
;
(2)點![]() ,
, ![]() .
.
(3),t的值為![]() ,
, ![]() 或
或![]() .
.
【解析】試題分析:
試題解析:( ![]() )
)![]() 代入
代入![]() 得
得![]() ,
,
∴一次函數表達式為![]() ,
,
∵![]() ,
,
∴![]()
∵![]() 軸,
軸,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
設![]() 的坐標為
的坐標為![]() ,代入二次函數
,代入二次函數![]() ,
,
解得![]() ,
, ![]() ,
,
∵![]() 在第一象限,
在第一象限,
∴![]() ,點
,點![]() ,
,
∵![]() 是二次函數
是二次函數![]() 的頂點,
的頂點,
∴![]() ,
,
設直線![]() 、
、![]() 解析式分別為
解析式分別為![]() ,
, ![]() ,
,
將![]() ,
, ![]() 代入直線
代入直線![]() 解析式得
解析式得![]() 解得
解得![]() .
.
將![]() ,
, ![]() 代入直線
代入直線![]() 解析式得
解析式得![]() ,解得
,解得![]() .
.
∴![]() ,
, ![]() .
.
(![]() )如圖所示,
)如圖所示, ![]() 與
與![]() 交點為
交點為![]() ,
,

過![]() 作
作![]() 軸的平行線
軸的平行線![]() ,
,
過![]() 作
作![]() 的垂線,交
的垂線,交![]() 于點
于點![]() ,連接
,連接![]() ,
,
設點![]() ,則
,則![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
∵![]() ,
,
![]() 且比值為常數,
且比值為常數,
當![]() 最大時,
最大時, ![]() 的值也最大,
的值也最大,
![]() ,
,
當![]() 時,
時, ![]() 取最大值,
取最大值,
![]() 也最大,此時點
也最大,此時點![]() .
.
代入二次函數得![]() ,
,
得![]() 或
或![]() (舍),
(舍),
∴![]() ,
,
令![]() ,得
,得![]() ,
,
![]() ,
,
![]() 為等腰直角三角形,
為等腰直角三角形, ![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 為等腰直角三角形,
為等腰直角三角形, ![]() ,
,
要使![]() 的值最小,即使
的值最小,即使![]() 的值最小,
的值最小,
當![]() 垂直
垂直![]() 時,
時, ![]() 的值最小,
的值最小,
此時![]() ,代入直線
,代入直線![]() 解析式得
解析式得![]() ,
,
∴點![]() ,
,
![]() .
.
(![]() )如圖所示,直線
)如圖所示,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,過
,過![]() 作
作![]() 軸的垂線,垂足為
軸的垂線,垂足為![]() ,
,

令![]() ,可求得
,可求得![]() ,
, ![]() 的坐標為
的坐標為![]() .
.
![]() ,
,
 ,
,
設橫坐標平移![]() ,縱坐標平移
,縱坐標平移![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
①當![]() 時,
時,
![]() .
.
②當![]() 時,
時,
![]() ,解得
,解得![]() .
.
![]() .
.
③當![]() 時,
時,
![]() ,解得
,解得![]() ,
,
![]() ,
,
綜上所述, ![]() 的值為
的值為![]() ,
, ![]() 或
或![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=2,BC=1,動點P從點B出發,沿路線B→C→D作勻速運動,那么△APB的面積S與點P運動的路程之間的函數圖象大致是( )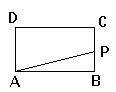
A.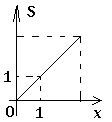
B.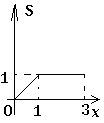
C.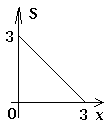
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,是拋物線y=ax2+bx+c(a≠0)圖象的一部分,已知拋物線的對稱軸為x=2,與x軸的一個交點是(﹣1,0).下列結論:
①ac<0;②4a﹣2b+c>0;③拋物線與x軸的另一個交點是(4,0);
④點(﹣3,y1),(6,y2)都在拋物線上,則有y1<y2.其中正確的個數為( )
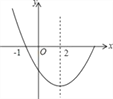
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC和△DBE中,BC=BE,還需再添加兩個條件才能使△ABC≌△DBE,則不能添加的一組條件是( )
A.AB=DB,∠ A=∠ D
B.DB=AB,AC=DE
C.AC=DE,∠C=∠E
D.∠ C=∠ E,∠ A=∠ D
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=x2+bx+c與x軸相交于A、B兩點,點B的坐標為(3,0),與y軸相交于點C(0,﹣3),頂點為D.
(1)求出拋物線y=x2+bx+c的表達式;
(2)連結BC,與拋物線的對稱軸交于點E,點P為線段BC上的一個動點,過點P作PF∥DE交拋物線于點F,設點P的橫坐標為m.
①當m為何值時,四邊形PEDF為平行四邊形.
②設四邊形OBFC的面積為S,求S的最大值.
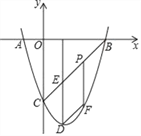
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知⊙![]() 的半徑為
的半徑為![]() ,
, ![]() 為直徑,
為直徑, ![]() 為弦.
為弦. ![]() 與
與![]() 交于點
交于點![]() ,將
,將![]() 沿著
沿著![]() 翻折后,點
翻折后,點![]() 與圓心
與圓心![]() 重合,延長
重合,延長![]() 至
至![]() ,使
,使![]() ,鏈接
,鏈接![]() .
.
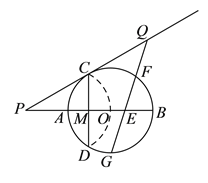
(![]() )求
)求![]() 的長.
的長.
(![]() )求證:
)求證: ![]() 是⊙
是⊙![]() 的切線.
的切線.
(![]() )點
)點![]() 為
為![]() 的中點,在
的中點,在![]() 延長線上有一動點
延長線上有一動點![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() (
(![]() 與
與![]() 、
、![]() 不重合).則
不重合).則![]() 為一定值.請說明理由,并求出該定值.
為一定值.請說明理由,并求出該定值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校籃球隊13名同學的身高如下表:
身高(cm) | 175 | 180 | 182 | 185 | 188 |
人數(個) | 1 | 5 | 4 | 2 | 1 |
則該校籃球隊13名同學身高的眾數和中位數分別是( )
A.182,180
B.180,180
C.180,182
D.188,182
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com