【題目】如圖1是實驗室中的一種擺動裝置，
在地面上，支架
是底邊為的等腰直角三角形，擺動臂長
可繞點
旋轉，擺動臂
可繞點
旋轉，
，
.
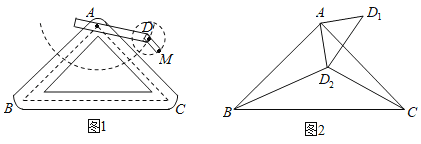
（1）在旋轉過程中：
①當
三點在同一直線上時，求
的長；
②當三點在同一直角三角形的頂點時，求的長.
（2）若擺動臂順時針旋轉
，點的位置由
外的點
轉到其內的點
處，連結
，如圖2，此時
，
，求
的長.
科目：初中數學 來源： 題型：
【題目】如圖1，矩形ABCD中，AD＝2，AB＝3，點E，F分別在邊AB，BC上，且BF＝FC，連接DE，EF，并以DE，EF為邊作DEFG．
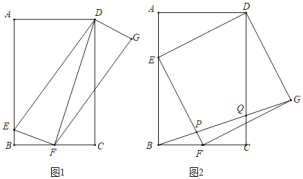
（1）連接DF，求DF的長度；
（2）求DEFG周長的最小值；
（3）當DEFG為正方形時（如圖2），連接BG，分別交EF，CD于點P、Q，求BP：QG的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知△ABC，以AC為直徑的⊙O交AB于點D，點E為弧AD的中點，連接CE交AB于點F，且BF=BC．
（1）求證：BC是⊙O的切線；
（2）若⊙O的半徑為2，
=
，求CE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖
，已知
、
、
、
、
是
上五點，的直徑
，
．為
的中點，延長
到點
．使
，連接
．
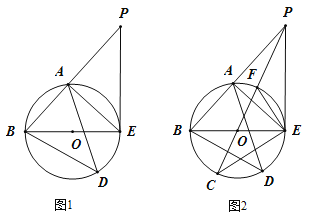
(1)求線段
的長；
(2)求證：直線是的切線．
(3)如圖
，連
交于點
，延長交PO交于另一點，連
、
，求
的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】二次函數圖象是拋物線，拋物線是指平面內到一個定點
和一條定直線
距離相等的點的軌跡．其中定點叫拋物線的焦點，定直線叫拋物線的準線．
①拋物線
(
)的焦點為
，例如，拋物線
的焦點是
；拋物線
的焦點是___________；
②將拋物線()向右平移
個單位、再向上平移
個單位(
，
)，可得拋物線
；因此拋物線的焦點是
．例如，拋物線
的焦點是
；拋物線
的焦點是_____________________．根據以上材料解決下列問題：
（1）完成題中的填空；
（2）已知二次函數的解析式為
；
①求其圖象的焦點的坐標；
②求過點且與
軸平行的直線與二次函數圖象交點的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某中學課外興趣活動小組準備圍建一個矩形苗圃，其中一邊靠墻，另外三邊用長為30米的籬笆圍成．已知墻長為18米(如圖所示)，設這個苗圃垂直于墻的一邊長為x米．
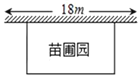
(1)若苗圃的面積為72平方米，求x的值；
(2)這個苗圃的面積能否是120平方米？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某水果經銷商到大圩種植基地采購葡萄，經銷商一次性采購葡萄的采購單價y（元/千克）與采購量x（千克）之間的函數關系圖象如圖中折線AB→BC→CD所示（不包括端點A），
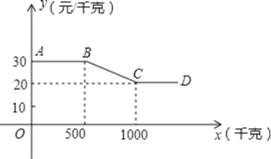
（1）當500＜x≤1000時，寫出y與x之間的函數關系式；
（2）葡萄的種植成本為8元/千克，某經銷商一次性采購葡萄的采購量不超過1000千克，當采購量是多少時，大圩種植基地獲利最大，最大利潤是多少元？
（3）在（2）的條件下，若經銷商一次性付了16800元貨款，求大圩種植基地可以獲得多少元的利潤？
查看答案和解析>>
科目：初中數學 來源： 題型：
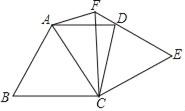
【題目】如圖，將等邊△ABC繞點C順時針旋轉90°得到△EFC，∠ACE的平分線CD交EF于點D，連接AD、AF．
（1）求∠CFA度數；
（2）求證：AD∥BC．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
