
【題目】如圖,矩形EFGH的四個(gè)頂點(diǎn)分別在矩形ABCD的各條邊上,AB=EF,FG=2,GC=3.有以下四個(gè)結(jié)論:①∠BGF=∠CHG;②△BFG≌△DHE;③tan∠BFG=![]() ;④矩形EFGH的面積是4
;④矩形EFGH的面積是4![]() .其中一定成立的是______.(把所有正確結(jié)論的序號填在橫線上)
.其中一定成立的是______.(把所有正確結(jié)論的序號填在橫線上)
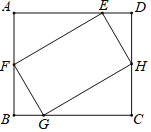
【答案】①②④
【解析】
根據(jù)矩形的性質(zhì)和同角的余角相等可判定①;根據(jù)AAS可判定②;先證△BFG∽△CGH,根據(jù)相似三角形的性質(zhì)及勾股定理判定③;由③中求得的數(shù)據(jù)結(jié)合已知,根據(jù)矩形面積公式判定④.
∵∠FGH=90°,∴∠BGF+∠CGH=90°.
又∵∠CGH+∠CHG=90°,
∴∠BGF=∠CHG,故①正確.
同理可得∠DEH=∠CHG.
∴∠BGF=∠DEH.
又∵∠B=∠D=90°,FG=EH,
∴△BFG≌△DHE,故②正確.
同理可得△AFE≌△CHG.
∴AF=CH.
易得△BFG∽△CGH.
設(shè)GH、EF為a,
∴![]()
∴![]()
∴BF=![]()
∴AF=AB﹣BF=a﹣![]()
∴CH=AF=a﹣![]() .
.
在Rt△CGH中,
∵CG2+CH2=GH2,
∴32+(a﹣![]() )2=a2.解得a=2
)2=a2.解得a=2![]() .
.
∴GH=2![]() .
.
∴BF=a﹣![]() =
=![]() .
.
在Rt△BFG中,∵cos∠BFG=![]() =
=![]() ,∴∠BFG=30°.
,∴∠BFG=30°.
∴tan∠BFG=tan30°=![]() ,故③錯(cuò)誤.
,故③錯(cuò)誤.
矩形EFGH的面積=FG×GH=2×2![]() =4
=4![]() ,故④正確.
,故④正確.
故答案為:①②④


 學(xué)練快車道快樂假期暑假作業(yè)新疆人民出版社系列答案
學(xué)練快車道快樂假期暑假作業(yè)新疆人民出版社系列答案 浙大優(yōu)學(xué)小學(xué)年級銜接導(dǎo)與練浙江大學(xué)出版社系列答案
浙大優(yōu)學(xué)小學(xué)年級銜接導(dǎo)與練浙江大學(xué)出版社系列答案 小學(xué)暑假作業(yè)東南大學(xué)出版社系列答案
小學(xué)暑假作業(yè)東南大學(xué)出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業(yè)江西人民出版社系列答案
波波熊暑假作業(yè)江西人民出版社系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
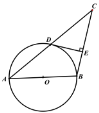
【題目】如圖,以△ABC的邊AB為直徑作⊙O經(jīng)過AC的中點(diǎn)D,然后過點(diǎn)D作DE⊥BC,垂足為點(diǎn)E.
(1)求證:DE是⊙O的切線;
(2)若⊙O的直徑為10,![]() ,求線段BE的長度.
,求線段BE的長度.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在“弘揚(yáng)傳統(tǒng)文化,打造書香校園”的活動(dòng)中,學(xué)校計(jì)劃開展四項(xiàng)活動(dòng):“A﹣國學(xué)誦讀”,“B﹣演講”,“C﹣課本劇”,“D﹣書法”,要求每位同學(xué)必須且只能參加其中一項(xiàng)活動(dòng),學(xué)校為了了解學(xué)生的意愿,隨機(jī)調(diào)查了部分學(xué)生,結(jié)果統(tǒng)計(jì)如圖:
(1)如圖,則被調(diào)查的總?cè)藬?shù)為 人;扇形統(tǒng)計(jì)圖中,希望參加活動(dòng)A所占圓心角為 度.
(2)根據(jù)題中信息補(bǔ)全條形統(tǒng)計(jì)圖;
(3)學(xué)校現(xiàn)有1000名學(xué)生,請根據(jù)圖中信息,估算全校學(xué)生希望參加活動(dòng)D有多少人?

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
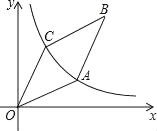
【題目】如圖,反比例函數(shù)![]() 在第一象限內(nèi)的圖象經(jīng)過菱形OABC的頂點(diǎn)A和C.若菱形OABC的面積為10,∠AOC=30°,則k的值為_____.
在第一象限內(nèi)的圖象經(jīng)過菱形OABC的頂點(diǎn)A和C.若菱形OABC的面積為10,∠AOC=30°,則k的值為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知下列命題:①已知菱形的兩條對角線長分別是a、b,則這個(gè)菱形的面積為![]() ab;②在Rt△ABC中,∠C=90°,若∠A>∠B,則cosA<cosB;③若m=n+1,則1﹣m2+2mn﹣n2=0;④若點(diǎn)A(x1,y1)和點(diǎn)B(x2,y2)在二次函數(shù)y=x2﹣2x﹣1的圖象上,且滿足x1>x2>1,則y2>y1>﹣2;其中假命題的個(gè)數(shù)是( )
ab;②在Rt△ABC中,∠C=90°,若∠A>∠B,則cosA<cosB;③若m=n+1,則1﹣m2+2mn﹣n2=0;④若點(diǎn)A(x1,y1)和點(diǎn)B(x2,y2)在二次函數(shù)y=x2﹣2x﹣1的圖象上,且滿足x1>x2>1,則y2>y1>﹣2;其中假命題的個(gè)數(shù)是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
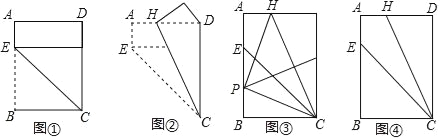
【題目】對給定的一張矩形紙片ABCD進(jìn)行如下操作:先沿CE折疊,使點(diǎn)B落在CD邊上(如圖①),再沿CH折疊,這時(shí)發(fā)現(xiàn)點(diǎn)E恰好與點(diǎn)D重合(如圖②)
(1)根據(jù)以上操作和發(fā)現(xiàn),求![]() 的值;
的值;
(2)將該矩形紙片展開.
①如圖③,折疊該矩形紙片,使點(diǎn)C與點(diǎn)H重合,折痕與AB相交于點(diǎn)P,再將該矩形紙片展開.求證:∠HPC=90°;
②不借助工具,利用圖④探索一種新的折疊方法,找出與圖③中位置相同的P點(diǎn),要求只有一條折痕,且點(diǎn)P在折痕上,請簡要說明折疊方法.(不需說明理由)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,小明在自家樓頂上的點(diǎn)A處測量建在與小明家樓房同一水平線上鄰居的電梯樓的高度,測得電梯樓頂部B處的仰角為60°,底部C處的俯角為26°,已知小明家樓房的高度AD=15米,求電梯樓的高度BC.(結(jié)果精確到0.1米,參考數(shù)據(jù):![]() ≈1.73,sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)
≈1.73,sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)
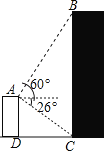
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方形網(wǎng)格中,每個(gè)小正方形的邊長都是一個(gè)單位長度,在平面直角坐標(biāo)系內(nèi),△ABC的三個(gè)頂點(diǎn)坐標(biāo)分別為A(1,4),B(1,1),C(3,1).
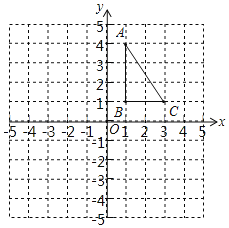
(1)畫出△ABC關(guān)于y軸對稱的△A1B1C1;
(2)畫出△ABC繞O點(diǎn)順時(shí)針旋轉(zhuǎn)90°后的△A2B2C2;
(3)在(2)的條件下,求點(diǎn)C劃過的路徑長度(結(jié)果保留π).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(本題滿分8分)某種電子產(chǎn)品共![]() 件,其中有正品和次品.已知從中任意取出一件,取得的產(chǎn)品為次品的概率為
件,其中有正品和次品.已知從中任意取出一件,取得的產(chǎn)品為次品的概率為![]() .
.
(1)該批產(chǎn)品有正品 件;
(2)如果從中任意取出![]() 件,利用列表或樹狀圖求取出
件,利用列表或樹狀圖求取出![]() 件都是正品的概率.
件都是正品的概率.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com