
【題目】我們定義:如圖1,在![]() 中,把
中,把![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 得到
得到![]() ,把
,把![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到
得到![]() ,連接
,連接![]() .當
.當![]() 時,我們稱
時,我們稱![]() 是
是![]() 的“旋補三角形”,
的“旋補三角形”,![]() 邊
邊![]() 上的中線
上的中線![]() 叫做
叫做![]() 的“旋補中線”.
的“旋補中線”.
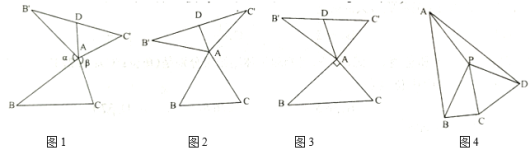
(特例感知)
(1)在圖2,圖3中,![]() 是
是![]() 的“旋補三角形”,
的“旋補三角形”,![]() 是
是![]() 的“旋補中線”.
的“旋補中線”.
①如圖2,當![]() 為等邊三角形,且
為等邊三角形,且![]() 時,則
時,則![]() 長為 .
長為 .
②如圖3,當![]() ,且
,且![]() 時,則
時,則![]() 長為 .
長為 .
(猜想論證)
(2)在圖1中,當![]() 為任意三角形時,猜想
為任意三角形時,猜想![]() 與
與![]() 的數量關系,并給予證明.(如果你沒有找到證明思路,可以考慮延長
的數量關系,并給予證明.(如果你沒有找到證明思路,可以考慮延長![]() 或延長
或延長![]() ,……)
,……)
(拓展應用)
(3)如圖4,在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,以
,以![]() 為邊在四邊形
為邊在四邊形![]() 內部作等邊
內部作等邊![]() ,連接
,連接![]() ,
,![]() .若
.若![]() 是
是![]() 的“旋補三角形”,請直接寫出
的“旋補三角形”,請直接寫出![]() 的“旋補中線”長及四邊形
的“旋補中線”長及四邊形![]() 的邊
的邊![]() 長.
長.
【答案】(1)①![]() ,②
,②![]() ;(2)
;(2)![]() ,見解析;(3)
,見解析;(3)![]() ,
,![]()
【解析】
(1)①由旋補三角形的概念可證明△ADB′是含有30°是直角三角形,可得AD=![]() BC即可解決問題;
BC即可解決問題;
②首先證明△BAC≌△B′AC′,根據直角三角形斜邊中線定理即可解決問題;
(2)結論:AD=![]() BC.如圖1中,延長AD到Q,使得AD=DQ,連接B′Q,C′Q,首先證明四邊形AC′QB′是平行四邊形,再證明△BAC≌△AB′Q,即可解決問題;
BC.如圖1中,延長AD到Q,使得AD=DQ,連接B′Q,C′Q,首先證明四邊形AC′QB′是平行四邊形,再證明△BAC≌△AB′Q,即可解決問題;
(3)由![]() ,
,![]() 是等邊三角形可得
是等邊三角形可得![]() ,由旋補三角形的概念可得
,由旋補三角形的概念可得![]() ,PB=PA,進而求出PB的長,再根據勾股定理就可求出BC的長,由(2)的結論即可求出旋補中線PE的長和AD的長.
,PB=PA,進而求出PB的長,再根據勾股定理就可求出BC的長,由(2)的結論即可求出旋補中線PE的長和AD的長.
解:(1)①∵![]() 是
是![]() 的“旋補三角形”,
的“旋補三角形”,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() 為等邊三角形,且
為等邊三角形,且![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 是等腰三角形,
是等腰三角形,![]() ,
,
∴AD⊥![]() ,
,![]() ,
,
∴AD=3,
②∵![]() 是
是![]() 的“旋補三角形”,
的“旋補三角形”,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵AD為中線,
∴![]() ;
;
(2)猜想:![]()
如圖,延長![]() 至Q,使
至Q,使![]() .
.
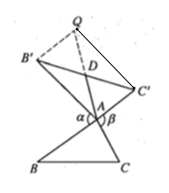
∵![]() 是
是![]() 的“旋補中線”,
的“旋補中線”,![]()
![]() .
.
![]() 四邊形
四邊形![]() 是平行四邊形,
是平行四邊形,
![]()
![]() ,
,![]()
![]()
![]() .
.
由定義可知![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]() .
.
∵![]() ,
,![]()
![]() ;
;
(3)過點P作PE⊥AB,取AD的中點F,連接PF,延長DP,過點A作AM⊥DM,如圖,
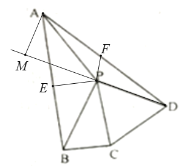
∵![]() ,△PCD是等邊三角形,
,△PCD是等邊三角形,
∴![]() ,
,
∵CD=6,
∴PC=CD=PD=6,
∵![]() 是
是![]() 的“旋補三角形”,
的“旋補三角形”,
∴![]() ,PB=PA,
,PB=PA,![]() ,
,
∴△PAB是等腰三角形,![]() ,
,
∵PE⊥AB,
∴EB=EA
∵AB=12,
∴BE=6,![]() ,
,
在△PBC中,由勾股定理得,
![]() ,
,
由(2)可知,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴MD=12,
在△AMD中,由勾股定理得,
∴![]() .
.


科目:初中數學 來源: 題型:
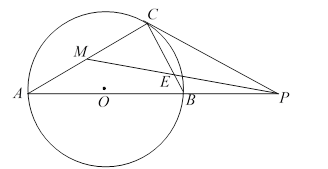
【題目】如圖,已知![]() 為
為![]() 的直徑,
的直徑,![]() 為
為![]() 延長線上的動點,過點
延長線上的動點,過點![]() 作
作![]() 的切線
的切線![]() ,
,![]() 為切點,
為切點, ![]() 為
為![]() 上的動點,連接
上的動點,連接![]() 交
交![]() 于點
于點![]() .
.
(1)當![]() 平分
平分![]() 時,求證:
時,求證:![]() ;
;
(2)當![]() 是
是![]() 的中點時,求證:
的中點時,求證:![]() ;
;
(3)當![]() ,且
,且![]() 的周長被
的周長被![]() 平分時,設
平分時,設![]() ,試求
,試求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
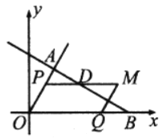
【題目】如圖,在![]() 中,
中,![]() ,點
,點![]() 的坐標為
的坐標為![]() ,
,![]() ,
,![]() 、
、![]() 分別是射線
分別是射線![]() 、線段
、線段![]() 上的點,且
上的點,且![]() ,以
,以![]() 、
、![]() 為鄰邊構造平行四邊形
為鄰邊構造平行四邊形![]() ,①若線段
,①若線段![]() 與
與![]() 交于點
交于點![]() ,當
,當![]() 時,則
時,則![]() _______;②把
_______;②把![]() 沿著
沿著![]() 進行折疊,當折疊后
進行折疊,當折疊后![]() 與
與![]() 的重疊部分的面積是平行四邊形
的重疊部分的面積是平行四邊形![]() 的
的![]() 時,則
時,則![]() _______.
_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
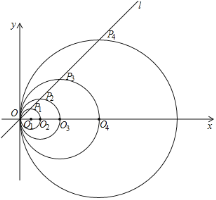
【題目】如圖,在平面直角坐標系中,直線l的函數表達式為y=x,點O1的坐標為(1,0),以O1為圓心,O1O為半徑畫圓,交直線l于點P1,交x軸正半軸于點O2;以O2為圓心,O2O為半徑畫圓,交直線l于點P2,交x軸正半軸于點O3;以O3為圓心,O3O為半徑畫圓,交直線l于點P3,交x軸正半軸于點O4;…按此做法進行下去,其中![]() 的長___________.
的長___________.
查看答案和解析>>
科目:初中數學 來源: 題型:
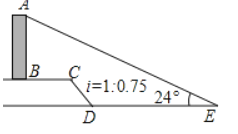
【題目】如圖,![]() 是一垂直于水平面的建筑物,某同學從建筑物底端
是一垂直于水平面的建筑物,某同學從建筑物底端![]() 出發,先沿水平方向向右行走
出發,先沿水平方向向右行走![]() 米到達點
米到達點![]() 再經過段坡度(或坡比)為
再經過段坡度(或坡比)為![]() 坡長為
坡長為![]() 米的斜坡
米的斜坡![]() 到達點
到達點![]() 然后再沿水平方向向右行走
然后再沿水平方向向右行走![]() 米到達點
米到達點![]() 均在同一平面內).在
均在同一平面內).在![]() 處測得建筑物頂端
處測得建筑物頂端![]() 的仰角為
的仰角為![]() 求建筑物
求建筑物![]() 的高度. (參考數據:
的高度. (參考數據:![]() ,
,![]()
![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
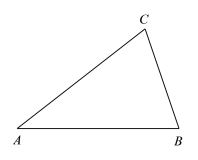
【題目】如圖,已知△ABC中,AB=AC.
(1)把△ABC繞點C順時針旋轉得到△DEC,使得點B的對應點E落在AB邊上,用尺規作圖的方法作出△DEC;(保留作圖痕跡,不寫作法)
(2)在(1)的條件下,連接AD,求證:AD=BC.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一只拉桿式旅行箱(圖1),其側面示意圖如圖2所示,已知箱體長AB=50cm,拉桿BC的伸長距離最大時可達35cm,點A,B,C在同一條直線上,在箱體底端裝有圓形的滾筒輪⊙A,⊙A與水平地面相切于點D,在拉桿伸長到最大的情況下,當點B距離水平地面34cm時,點C到水平地面的距離CE為55cm.設AF∥ MN.
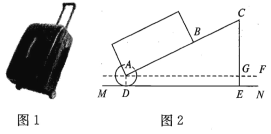
(1)求⊙A的半徑.
(2)當人的手自然下垂拉旅行箱時,人感到較為舒服,某人將手自然下垂在C端拉旅行箱時,CE為76cm,∠CAF=64°,求此時拉桿BC的伸長距離(結果精確到1cm,參考數據:sin64°≈0.9,cos64°≈0.39,tan64°≈2.1).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com