
【題目】在學習了數軸后,小亮決定對數軸進行變化應用:
(1)應用一:已知點A在數軸上表示為![]() ,數軸上任意一點B表示的數為
,數軸上任意一點B表示的數為![]() ,則AB兩點的距離可以表示為 ;應用這個知識,請寫出當
,則AB兩點的距離可以表示為 ;應用這個知識,請寫出當![]() 時,
時,![]() 有最小值為 .
有最小值為 .
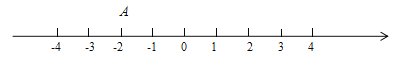
(2)應用二:從數軸上取下一個單位長度的線段,第一次剪掉原長的![]() ,第二次剪掉剩下的
,第二次剪掉剩下的![]() ,依次類推,每次都剪掉剩下的
,依次類推,每次都剪掉剩下的![]() ,則剪掉5次后剩下線段長度為 ;應用這個原理,請計算:
,則剪掉5次后剩下線段長度為 ;應用這個原理,請計算:![]() .
.
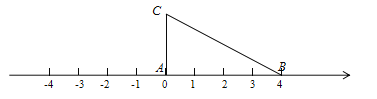
(3)應用三:如圖,將一根拉直的細線看作數軸,一個三邊長分別為![]() 的三角形
的三角形![]() 的頂點
的頂點![]() 與原點重合,
與原點重合,![]() 邊在數軸正半軸上,將數軸正半軸的線沿
邊在數軸正半軸上,將數軸正半軸的線沿![]() 的順序依次纏繞在三角形
的順序依次纏繞在三角形![]() 的邊上,負半軸的線沿
的邊上,負半軸的線沿![]() 的順序依次纏繞在三角形
的順序依次纏繞在三角形![]() 的邊上.
的邊上.
①如果正半軸的線纏繞了5圈,負半軸的線纏繞了3圈,求繞在點![]() 上的所有數之和;
上的所有數之和;
②如果正半軸的線不變,將負半軸的線拉長一倍,即原線上的點![]() 的位置對應著拉長后的數
的位置對應著拉長后的數![]() ,并將三角形
,并將三角形![]() 向正半軸平移一個單位后再開始繞,求繞在點
向正半軸平移一個單位后再開始繞,求繞在點![]() 且絕對值不超過100的所有數之和.
且絕對值不超過100的所有數之和.
【答案】(1)![]()
![]() (2)
(2)![]() (3)①
(3)①![]() ②
②![]()
【解析】
(1)根據數軸上兩點間的距離的表示列出式子即可;
(2)第1次剪掉的長度是![]() ;第1次剪掉后剩下的長度是
;第1次剪掉后剩下的長度是![]()
第2次剪掉的長度是![]() 第2次剪掉后剩下的長度是
第2次剪掉后剩下的長度是![]()
第3次剪掉的長度是![]() ;第3次剪掉后剩下的長度是
;第3次剪掉后剩下的長度是![]() …由此規律得出:第7次剪掉后剩下的長度是
…由此規律得出:第7次剪掉后剩下的長度是![]() ;即可求出
;即可求出![]() .
.
(3)①分別找出正半軸以及負半軸在點![]() 上的數字之間的規律,即可求出所有數字之和.
上的數字之間的規律,即可求出所有數字之和.
②繞在點![]() 且絕對值不超過100的所有數,求和即可.
且絕對值不超過100的所有數,求和即可.
(1)已知點A在數軸上表示為![]() ,數軸上任意一點B表示的數為
,數軸上任意一點B表示的數為![]() ,則AB兩點的距離可以表示為
,則AB兩點的距離可以表示為![]() 應用這個知識,當
應用這個知識,當![]()
![]() 時,
時,![]() 有最小值為8.
有最小值為8.
故答案為:![]()
![]()
(2)第1次剪掉的長度是![]() ;第1次剪掉后剩下的長度是
;第1次剪掉后剩下的長度是![]()
第2次剪掉的長度是![]() 第2次剪掉后剩下的長度是
第2次剪掉后剩下的長度是![]()
第3次剪掉的長度是![]() ;第3次剪掉后剩下的長度是
;第3次剪掉后剩下的長度是![]() …由此規律得出第5次剪掉剩下的長度是
…由此規律得出第5次剪掉剩下的長度是![]() ,…第7次剪掉后剩下的長度是
,…第7次剪掉后剩下的長度是![]() ;
;
所以第5次剪掉剩下的長度是![]()
則![]()
(3)①如果正半軸的線纏繞了5圈,繞在點C的數字分別為:![]()
負半軸的線纏繞了3圈,繞在點![]() 上的數字分別為:
上的數字分別為:![]()
則繞在點![]() 上的所有數之和為:
上的所有數之和為:![]()
②如果正半軸的線不變,并將三角形![]() 向正半軸平移一個單位后再開始繞,則正半軸上繞在點
向正半軸平移一個單位后再開始繞,則正半軸上繞在點![]() 且絕對值不超過100的數字有:
且絕對值不超過100的數字有:![]()
將負半軸的線拉長一倍,并將三角形![]() 向正半軸平移一個單位后再開始繞,正半軸上繞在點
向正半軸平移一個單位后再開始繞,正半軸上繞在點![]() 且絕對值不超過100的數字有:
且絕對值不超過100的數字有:![]()
![]()
繞在點![]() 且絕對值不超過100的所有數之和為:
且絕對值不超過100的所有數之和為:![]()


 新課標同步訓練系列答案
新課標同步訓練系列答案 一線名師口算應用題天天練一本全系列答案
一線名師口算應用題天天練一本全系列答案科目:初中數學 來源: 題型:
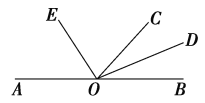
【題目】如圖,O是直線AB上一點,OC為任意一條射線,OD平分∠BOC,OE平分∠AOC.
(1)OD與OE的位置關系是______;(2)∠EOC的余角是_______ .
查看答案和解析>>
科目:初中數學 來源: 題型:
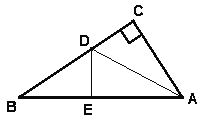
【題目】如圖,有一個直角三角形紙片,兩直角邊AC=6cm,BC=8cm,現將直角邊AC沿直線AD折疊,使它落在斜邊AB上,且與AE重合,你能求出CD的長嗎?若能,請給出求解過程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,AC是⊙O的切線,BC與⊙O相交于點D,點E在⊙O上,且DE=DA,AE與BC相交于點F.
(1)求證:FD=DC;
(2)若AE=8,DE=5,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,BC交⊙O于點D,DE⊥AC于點E,要使DE是⊙O的切線,還需補充一個條件,則補充的條件不正確的是( ) 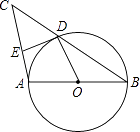
A.DE=DO
B.AB=AC
C.CD=DB
D.AC∥OD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某檢修小組從![]() 地出發,在東西向的馬路上檢修線路,如果規定向東行駛為正,向西行駛為負,一天中七次行駛紀錄如下.(單位:
地出發,在東西向的馬路上檢修線路,如果規定向東行駛為正,向西行駛為負,一天中七次行駛紀錄如下.(單位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
![]() 求收工時,檢修小組在
求收工時,檢修小組在![]() 地的哪個方向?距離
地的哪個方向?距離![]() 地多遠?
地多遠?
![]() 在第幾次紀錄時距
在第幾次紀錄時距![]() 地最遠?
地最遠?
![]() 若汽車行駛每千米耗油
若汽車行駛每千米耗油![]() 升,問從
升,問從![]() 地出發,檢修結束后再回到
地出發,檢修結束后再回到![]() 地共耗油多少升?
地共耗油多少升?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,梯形ABCD中,AD∥BC,BC=20cm,AD=10cm,現有兩個動點P、Q分別從B、D兩點同時出發,點P以每秒2cm的速度沿BC向終點C移動,點Q以每秒1cm的速度沿DA向終點A移動,線段PQ與BD相交于點E,過E作EF∥BC交CD于點F,射線QF交BC的延長線于點H,設動點P、Q移動的時間為t(單位:秒,0<t<10). 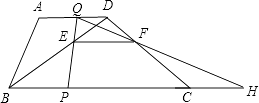
(1)當t為何值時,四邊形PCDQ為平行四邊形?
(2)在P、Q移動的過程中,線段PH的長是否發生改變?如果不變,求出線段PH的長;如果改變,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料:小明在學習二次根式后,發現一些含根號的式子可以寫成另一個式子的平方,如3+2![]() =(1+
=(1+![]() )2.善于思考的小明進行了以下探索:設a+b
)2.善于思考的小明進行了以下探索:設a+b![]() =(m+n
=(m+n![]() )2(其中a,b,m,n均為整數),則有a+b
)2(其中a,b,m,n均為整數),則有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() ,∴a=m2+2n2,b=2mn.這樣小明就找到了一種把類似a+b
,∴a=m2+2n2,b=2mn.這樣小明就找到了一種把類似a+b![]() 的式子化為平方式的方法.請你仿照小明的方法解決下列問題:
的式子化為平方式的方法.請你仿照小明的方法解決下列問題:
(1)當a,b,m,n均為正整數時,若a+b![]() =(m+n
=(m+n![]() )2,用含m,n的式子分別表示a,b,得a=______________,b=________;
)2,用含m,n的式子分別表示a,b,得a=______________,b=________;
(2)利用所探索的結論,找一組正整數a,b,m,n填空:
________+________![]() =(________+________
=(________+________![]() )2;
)2;
(3)若a+4![]() =(m+n
=(m+n![]() )2,且a,m,n均為正整數,求a的值.
)2,且a,m,n均為正整數,求a的值.
(4)試化簡![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com