Question

5．已知⊙A和⊙B相交于C、D．且它們都與⊙O內切，切點分別為M（M在⊙A上）、N．射線CD交⊙O于點P．PM交⊙A于點E，PN交⊙B于點F，求證：EF是⊙A、⊙B的公切線．

Answer 1

分析 如圖，連接OP、OM、ON、MN、AE、BF，則O、A、M共線，O、B、N共線．只要證明∠PFE+∠4=90°，BF∥AE即可解決問題．

解答 證明：如圖，連接OP、OM、ON、MN、AE、BF，則O、A、M共線，O、B、N共線．
∵OP=ON=OM，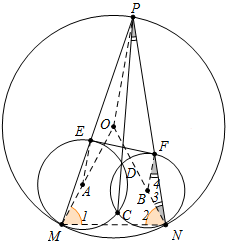
∴∠1=∠2，∠OPN=∠3，∠OMP=∠OPM，
∵2∠OMP+2∠1+2∠3=180°
∴∠OMP+∠1+∠3=90°，
∵PD•PC=PE•PM=PF•PN，
∴$\frac{PF}{PM}$=$\frac{PE}{PN}$，∵∠EPF=∠NPM，
∴△PEF∽△PNM，
∴∠PFE=∠PMN，
∵BF=BN，
∴∠3=∠4，
∴∠PFE+∠4=∠OMP+∠1+∠3=90°，
∴∠EFB=90°，
∵AM=AE，OM=OP，
∴∠AME=∠AEM=∠OPM，
∴AE∥OP，同理BF∥OP，
∴AE∥BF，
∴∠AEF+∠EFB=180°，
∴∠FEA=∠EFB=90°，
∴EF是⊙A，⊙B的公切線．

點評 本題考查切線的判定、圓的有關知識、三角形內角和定理，平行線的性質等知識，解題的關鍵是學會添加常用輔助線，構造等腰三角形解決問題，題目比較難，輔助線比較多，屬于競賽題目．