
【題目】如圖,在Rt△ABC中,∠C=90°,BD平分∠ABC,與AC交于點D,點O是AB上一點,⊙O過B、D兩點,且分別交AB、BC于點E、F.
(1)求證:AC是⊙O的切線;
(2)已知AB=10,BC=6,求⊙O的半徑r .
【答案】
(1)證明:連接OD. 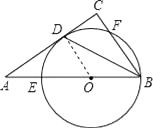
∵OB=OD,
∴∠OBD=∠ODB(等角對等邊);
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ODB=∠DBC(等量代換),
∴OD∥BC(內錯角相等,兩直線平行);
又∵∠C=90°(已知),
∴∠ADO=90°(兩直線平行,同位角相等),
∴AC⊥OD,即AC是⊙O的切線;
(2)解:由(1)知,OD∥BC,
∴ ![]() (平行線截線段成比例),
(平行線截線段成比例),
∴ ![]() ,
,
解得r= ![]() ,即⊙O的半徑r為
,即⊙O的半徑r為 ![]() .
.
【解析】根據等角對等邊得到∠OBD=∠ODB,由角平分線的定義和等量代換,得到兩直線平行,根據兩直線平行,同位角相等得到AC是⊙O的切線;(2)由(1)知,OD∥BC,根據平行線截線段成比例定理,兩條直線被一組平行線所截,截得的對應線段的長度成比例;求出⊙O的半徑.
【考點精析】認真審題,首先需要了解切線的判定定理(切線的判定方法:經過半徑外端并且垂直于這條半徑的直線是圓的切線),還要掌握平行線分線段成比例(三條平行線截兩條直線,所得的對應線段成比例)的相關知識才是答題的關鍵.


 小學課時特訓系列答案
小學課時特訓系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=x2+bx+c與坐標軸交于A,B兩點,則一元二次方程x2+bx+c=0的根的情況是( )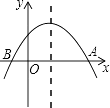
A.沒有實數根
B.有兩個相等的實數根
C.有兩個不相等的實數根
D.可能有實數根,也可能沒有實數根
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AD、BC是⊙O的兩條互相垂直的直徑,點P從點O出發,沿O→C→D→O的路線勻速運動,設∠APB=y(單位:度),那么y與點P運動的時間x(單位:秒)的關系圖是( )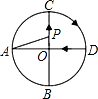
A.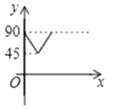
B.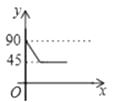
C.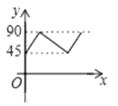
D.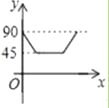
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠CDO=50°,則下列結論:①∠AOE=65°;②OF平分∠BOD;③∠GOE=∠DOF;④∠AOE=∠GOD.其中正確結論的個數是( )

A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC在直角坐標系中.
(1)寫出點A,點B的坐標A( , ),B( , );
(2)S△ABC= ;
(3)若把△ABC向上平移2個單位,再向右平移2個單位得△A1B1C1,在圖中畫出△A1B1C1的位置,并寫出點A1、B1、C1的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題1:現有一張△ABC紙片,點D、E分別是△ABC邊上兩點,若沿直線DE折疊.
(1)探究1:如果折成圖①的形狀,使A點落在CE上,則∠1與∠A的數量關系是 ;
(2)探究2:如果折成圖②的形狀,猜想∠1+∠2和∠A的數量關系是 ;
(3)探究3:如果折成圖③的形狀,猜想∠1、∠2和∠A的數量關系,并說明理由.

(4)問題2:將問題1推廣,如圖④,將四邊形ABCD紙片沿EF折疊,使點A、B落在四邊形EFCD的內部時,∠1+∠2與∠A、∠B之間的數量關系是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com