
【題目】如圖,Rt△OAC是一張放在平面直角坐標系中的直角三角形紙片,點O與原點重合,點A在x軸上,點C在y軸上,OA和OC是方程x![]() (3+
(3+![]() )x+3
)x+3![]() =0的兩根(OA>OC),∠CAO=30°,將Rt△OAC折疊,使OC邊落在AC邊上,點O與點D重合,折痕為CE.
=0的兩根(OA>OC),∠CAO=30°,將Rt△OAC折疊,使OC邊落在AC邊上,點O與點D重合,折痕為CE.
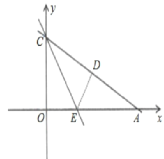
(1)求點D的坐標;
(2)設點M為直線CE上的一點,過點M作AC的平行線,交y軸于點N,是否存在這樣的點M,使得以M、N、D. C為頂點的四邊形是平行四邊形?若存在,請求出符合條件的點M的坐標;若不存在,請說明理由.
【答案】(1)D(![]() ,
,![]() );(2)M(
);(2)M(![]() ,
,![]() );
);
【解析】
(1)由折紙可以知道CD=OC,從而求出AD,作DF⊥OA于F解直角三角形可以求出D點的坐標.
(2)存在滿足條件的M點,利用三角形全等和平行線等分線段定理可以求出M點對應的坐標.
(1) 解方程x![]() (3+
(3+![]() )x+3
)x+3![]() =0得:
=0得:
x![]() =
=![]() ,x
,x![]() =3
=3
∵OA>OC
∴OA=3,OC=![]() ;
;
在Rt△AOC中,由勾股定理得:
AC=![]() =2
=2![]() ,
,
由軸對稱得:CO=CD=![]() ,作DF⊥OA于F,
,作DF⊥OA于F,
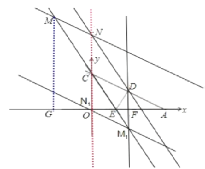
∴AD=![]() ,作DF⊥OA,且∠CAO=30°,
,作DF⊥OA,且∠CAO=30°,
∴DF=![]() ,由勾股定理得:
,由勾股定理得:
AF=![]() ,
,
∴OF=![]() ,∴OF=AF
,∴OF=AF
∴D(![]() ,
,![]() );
);
(2)∵M![]() N
N![]()
∠N![]() M
M![]() F=∠ADF,∠FN
F=∠ADF,∠FN![]() M
M![]() =∠FAD
=∠FAD
∵OF=AF
∴△ADF≌△N![]() M
M![]() F(AAS),
F(AAS),
∴M![]() F=DF=
F=DF=![]() ,N
,N![]() F=AF=
F=AF=![]() ,
,
∴M![]() (
(![]() ,
, ![]() ),作MG⊥OA,
),作MG⊥OA,
∵四邊形MCDN和四邊形CN![]() M
M![]() D是平行四邊形
D是平行四邊形
∴MC=ND,ND=CM![]() ∴MC=CM
∴MC=CM![]()
∴GO=OF=![]() ,OE=1
,OE=1
∴GE=![]() ,
,
∴EOC△∽△EGM
∴![]()
∴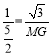 解得:
解得:
MG=![]() ,
,
∴M(![]() ,
,![]() )
)


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,等腰△ABC的周長為21,底邊BC=5,AB的垂直平分線DE交AB于點D,交AC于點E,則△BEC的周長為( )

A. 13B. 16C. 8D. 10
查看答案和解析>>
科目:初中數學 來源: 題型:
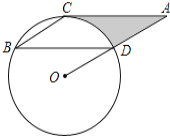
【題目】如圖,點B、C、D都在⊙O上,過C點作CA∥BD交OD的延長線于點A,連接BC,∠B=∠A=30°,BD=4![]() .
.
(1)求證:AC是⊙O的切線;
(2)求由線段AC、AD與弧CD所圍成的陰影部分的面積.(結果保留π)
查看答案和解析>>
科目:初中數學 來源: 題型:
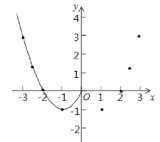
【題目】某班“數學興趣小組”對函數y=x![]() 2|x|的圖象和性質進行了探究,探究過程如下,請補充完整:
2|x|的圖象和性質進行了探究,探究過程如下,請補充完整:
(1)自變量x的取值范圍是全體實數,x與y的幾組對應值列表如下:
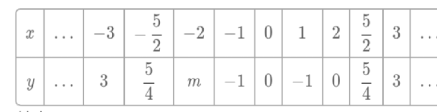
其中,m=___.
(2)根據表中數據,在如圖所示的平面直角坐標系中描點,并畫出了函數圖象的一部分,請畫出該函數圖象的另一部分.
(3)探究函數圖象發現:
①函數圖象與x軸有___個交點,所以對應的方程x![]() 2|x|=0有___個實數根;
2|x|=0有___個實數根;
②方程x![]() 2|x|=
2|x|=![]() 有___個實數根;
有___個實數根;
③關于x的方程x![]() 2|x|=a有4個實數根時,a的取值范圍是___.
2|x|=a有4個實數根時,a的取值范圍是___.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】三江夜游項目是寧波市月光經濟和“三江六岸”景觀提升的重要工程,一艘游輪從周宿夜江游船碼頭到寧波大劇院游船碼頭順流而行用40分鐘,從寧波大劇院游船碼頭沿原線返回周宿夜江游船碼頭用了1小時,已知游輪在靜水中的平均速度為8千米/小時,求水流的速度.設水流的速度為x千米/小時,則可列方程為( )
A.40(8-x)=1×(8+x) B.![]() (8+x)=8 C.
(8+x)=8 C.![]() (8+x)=8-x D.
(8+x)=8-x D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
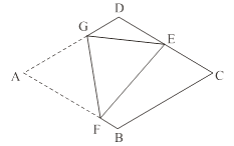
【題目】如圖,在菱形紙片ABCD中,AB=2,∠A=60°,將菱形紙片翻折,使點A落在CD的中點E處,折痕為FG,點F、G分別在邊AB、AD上.則cos∠EFG的值為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
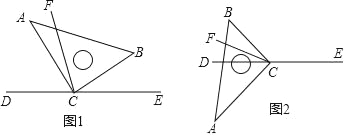
【題目】直角三角板ABC的直角頂點C在直線DE上,CF平分∠BCD.
(1)在圖1中,若∠BCE=40°,求∠ACF的度數;
(2)在圖1中,若∠BCE=α,直接寫出∠ACF的度數(用含α的式子表示);
(3)將圖1中的三角板ABC繞頂點C旋轉至圖2的位置,探究:寫出∠ACF與∠BCE的度數之間的關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
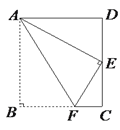
【題目】如圖,四邊形ABCD為矩形紙片,把紙片ABCD折疊,使點B恰好落在CD邊的中點E處, 折痕為AF,若CD=6,則AF等于__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com