
【題目】已知函數y=﹣![]() (x+1)2﹣2
(x+1)2﹣2
(1)指出函數圖象的開口方向是 ,對稱軸是 ,頂點坐標為
(2)當x 時,y隨x的增大而增大
(3)怎樣移動拋物線y=﹣![]() x2就可以得到拋物線y=﹣
x2就可以得到拋物線y=﹣![]() (x+1)2﹣2
(x+1)2﹣2
【答案】(1)開口方向向下、對稱軸為x=-1、頂點坐標為(-1,-2);(2)![]() ;(3)向左平移1個單位長度,再向下平移2個單位長度.
;(3)向左平移1個單位長度,再向下平移2個單位長度.
【解析】
(1)利用二次根式的性質確定出開口方向,頂點坐標以及對稱軸即可;
(2)由對稱軸和開口方向得出增減性;
(3)根據平移規律回答問題.
(1)∵a=-![]() <0,
<0,
∴拋物線開口向下,
頂點坐標為(-1,-2),對稱軸為直線x=-1;
故答案是:開口方向向下、對稱軸為x=-1、頂點坐標為(-1,-2);
(2)∵對稱軸x=-1,
∴當x<-1時,y隨x的增大而減大.
故答案是:![]() ;
;
(3)向左平移1個單位長度,再向下平移2個單位長度移動拋物線y=-![]() x2就可以得到拋物線y=-
x2就可以得到拋物線y=-![]() (x+1)2-2.
(x+1)2-2.


 名牌學校分層周周測系列答案
名牌學校分層周周測系列答案 黃岡海淀全程培優測試卷系列答案
黃岡海淀全程培優測試卷系列答案科目:初中數學 來源: 題型:
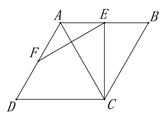
【題目】如圖,四邊形ABCD是邊長為2的菱形,E,F分別是AB,AD的中點,連接EF,EC,將△FAE繞點F旋轉180°得到△FDM.
(1)補全圖形并證明:EF⊥AC;
(2)若∠B=60°,求△EMC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是矩形,AB=8,BC=4,動點P以每秒2個單位的速度從點A沿線段AB向B點運動,同時動點Q以每秒3個單位的速度從點B出發沿B-C-D的方向運動,當點Q到達點D時P、Q同時停止運動,若記△PQA的面積為y,運動時間為x,則下列圖象中能大致表示y與x之間函數關系圖象的是( )
A.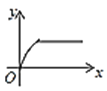 B.
B.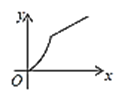 C.
C.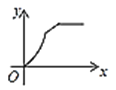 D.
D.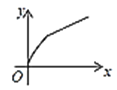
查看答案和解析>>
科目:初中數學 來源: 題型:
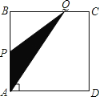
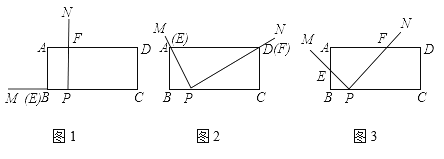
【題目】如圖1,在矩形ABCD中,AB=2,BC=5,BP=1,∠MPN=90°,將∠MPN繞點P從PB處開始順時針方向旋轉,PM交邊AB于點E,PN交邊AD于點F,當PE旋轉至PA處時,∠MPN的旋轉隨即停止.
(1)如圖2,在旋轉中發現當PM經過點A時,PN也經過點D,求證:△ABP ∽△PCD
(2)如圖3,在旋轉過程中,![]() 的值是否為定值?若是,請求出該定值;若不是,請說明理由
的值是否為定值?若是,請求出該定值;若不是,請說明理由
(3)設AE![]() ,連結EF,則在旋轉過程中,當
,連結EF,則在旋轉過程中,當![]() 為何值時,△BPE與△PEF相似.
為何值時,△BPE與△PEF相似.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解方程
(1)x2+1=3x
(2)(x﹣2)(x﹣3)=12
(3)(2x﹣3)2+x(2x﹣3)=0(因式分解法)
(4)2x2﹣4x﹣1=0(用配方法).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店購進一批單價為16元的日用品,銷售一段時間后,為了獲取更多利潤, 商店決定提高銷售價格,經試驗發現,若按每件20元的價格銷售時,每月能賣360件; 若按每件25元的價格銷售時,每月能賣210件.假定每月銷售件數y(件)是價格x( 元/件)的一次函數.
(1)試求y與x之間的函數關系式;
(2)在商品不積壓,且不考慮其他因素的條件下,問銷售價格為多少時,才能使每月獲得最大利潤?每月的最大利潤是多少?(總利潤=總收入-總成本).
查看答案和解析>>
科目:初中數學 來源: 題型:
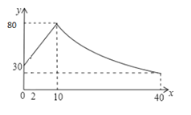
【題目】學生上課時注意力集中的程度可以用注意力指數表示.某班學生在一節數學課中的注意力指數![]() 隨上課時間
隨上課時間![]() (分鐘)的變化圖象如圖.上課開始時注意力指數為30,第10分鐘時注意力指數為80,前10分鐘內注意力指數
(分鐘)的變化圖象如圖.上課開始時注意力指數為30,第10分鐘時注意力指數為80,前10分鐘內注意力指數![]() 是時間
是時間![]() 的一次函數.10分鐘以后注意力指數
的一次函數.10分鐘以后注意力指數![]() 是
是![]() 的反比例函數.
的反比例函數.
(1)求出![]() 時和
時和![]() 時,求
時,求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(2)如果講解一道較難的數學題要求學生的注意力指數不小于50,為了保證教學效果本節課講完這道題不能超過多少分鐘?
查看答案和解析>>
科目:初中數學 來源: 題型:
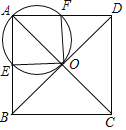
【題目】已知,如圖,正方形ABCD的對角線AC,BD相交于點O,點E為AB上一點(不與A.B兩點重合),過點O,A,E的⊙I交AD于F,AB=5
(1)求⊙I的直徑的取值范圍;
(2)若⊙I的半徑為2,求AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小田同學學習反比例函數![]() 的圖象和性質后,對新函數
的圖象和性質后,對新函數![]() 的圖象和性質進行了探究,以下是她的探究過程:.
的圖象和性質進行了探究,以下是她的探究過程:.
第一步:在直角坐標系中,作出函數![]() 的圖象;
的圖象;
第二步:通過列表、描點、連線,作出新函數![]() 的圖象
的圖象
①列表:
| … | -4 | -2 | -1 | 0 | 1 | 3 | 4 | 5 | 6 | … |
| … | 1 | 1.5 | 2 | 3 | 6 | -6 | -3 | -2 | -1.5 | … |
②描點:如圖所示.

(1)請在圖中,幫助小田同學完成連線的步驟;
(2)觀察圖象,發現函數![]() 與函數
與函數![]() 的圖象都是雙曲線,并且形狀也相同,只是位置發生了改變,由此可知,函數
的圖象都是雙曲線,并且形狀也相同,只是位置發生了改變,由此可知,函數![]() 的圖象可由函數
的圖象可由函數![]() 的圖象平移得到,請寫出函數
的圖象平移得到,請寫出函數![]() 的圖象是怎樣平移得到的?
的圖象是怎樣平移得到的?
(3)若點![]() ,
,![]() 在函數圖象
在函數圖象![]() 上,且
上,且![]() ,則
,則![]()
![]() (選填“>”“<”或“=”)
(選填“>”“<”或“=”)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com