
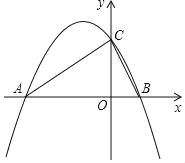
【題目】在平面直角坐標系中,二次函數y=ax2+bx+2的圖象與x軸交于A(﹣4,0),B (1,0)兩點,與y軸交于點C.
(1)求這個二次函數的解析式;
(2)連接AC、BC,判斷△ABC的形狀,并證明;
(3)若點P為二次函數對稱軸上點,求出使△PBC周長最小時,點P的坐標.
【答案】(1)拋物線解析式為y=﹣![]() x2﹣
x2﹣![]() x+2;(2)△ABC為直角三角形,理由見解析;(3)當P點坐標為(﹣
x+2;(2)△ABC為直角三角形,理由見解析;(3)當P點坐標為(﹣![]() ,
,![]() )時,△PBC周長最小
)時,△PBC周長最小
【解析】
(1)設交點式y=a(x+4)(x-1),展開得到-4a=2,然后求出a即可得到拋物線解析式;
(2)先利用兩點間的距離公式計算出AC2=42+22,BC2=12+22,AB2=25,然后利用勾股定理的逆定理可判斷△ABC為直角三角形;
(3)拋物線的對稱軸為直線x=-![]() ,連接AC交直線x=-
,連接AC交直線x=-![]() 于P點,如圖,利用兩點之間線段最短得到PB+PC的值最小,則△PBC周長最小,接著利用待定系數法求出直線AC的解析式為y=
于P點,如圖,利用兩點之間線段最短得到PB+PC的值最小,則△PBC周長最小,接著利用待定系數法求出直線AC的解析式為y=![]() x+2,然后進行自變量為-
x+2,然后進行自變量為-![]() 所對應的函數值即可得到P點坐標.
所對應的函數值即可得到P點坐標.
(1)拋物線的解析式為y=a(x+4)(x﹣1),
即y=ax2+3ax﹣4a,
∴﹣4a=2,解得a=﹣![]() ,
,
∴拋物線解析式為y=﹣![]() x2﹣
x2﹣![]() x+2;
x+2;
(2)△ABC為直角三角形.理由如下:
當x=0時,y=﹣![]() x2﹣
x2﹣![]() x+2=2,則C(0,2),
x+2=2,則C(0,2),
∵A(﹣4,0),B (1,0),
∴AC2=42+22,BC2=12+22,AB2=52=25,
∴AC2+BC2=AB2,
∴△ABC為直角三角形,∠ACB=90°;
(3)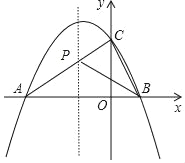
拋物線的對稱軸為直線x=﹣![]() ,
,
連接AC交直線x=﹣![]() 于P點,如圖,
于P點,如圖,
∵PA=PB,
∴PB+PC=PA+PC=AC,
∴此時PB+PC的值最小,△PBC周長最小,
設直線AC的解析式為y=kx+m,
把A(﹣4,0),C(0,2)代入得![]() ,解得
,解得![]() ,
,
∴直線AC的解析式為y=![]() x+2,
x+2,
當x=﹣![]() 時,y=
時,y=![]() x+2=
x+2=![]() ,則P(﹣
,則P(﹣![]() ,
,![]() )
)
∴當P點坐標為(﹣![]() ,
,![]() )時,△PBC周長最小.
)時,△PBC周長最小.


科目:初中數學 來源: 題型:
【題目】有一個二次函數的圖象,三位同學分別說出了它的一些特點:
甲:對稱軸為直線x=4
乙:與x軸兩個交點的橫坐標都是整數.
丙:與y軸交點的縱坐標也是整數,且以這三個點為頂點的三角形面積為3.請你寫出滿足上述全部特點的一個二次函數解析式__________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學舉辦“校園好聲音”朗誦大賽,根據初賽成績,七年級和八年級各選出5名選手組成七年級代表隊和八年級代表隊參加學校決賽兩個隊各選出的5名選手的決賽成績如圖所示:
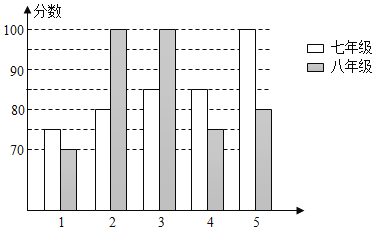
(1)根據所給信息填寫表格;
平均數(分) | 中位數(分) | 眾數(分) | |
七年級 | 85 | ||
八年級 | 85 | 100 |
(2)結合兩隊成績的平均數和中位數,分析哪個隊的決賽成績較好;
(3)若七年級代表隊決賽成績的方差為70,計算八年級代表隊決賽成績的方差,并判斷哪個代表隊的選手成績較為穩定.
查看答案和解析>>
科目:初中數學 來源: 題型:
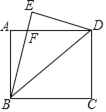
【題目】如圖,將矩形ABCD沿對角線BD折疊,使點C落在點E處,BE與AD交于點F.
(1)求證:△ABF≌△EDF;
(2)若AB=6,BC=8,求AF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
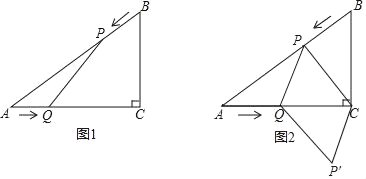
【題目】已知:如圖1在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,點P由點B出發沿BA方向向點A勻速運動,速度為2cm/s;同時點Q由點A出發沿AC方向點C勻速運動,速度為lcm/s;連接PQ,設運動的時間為t秒(0<t<5),解答下列問題:
(1)當為t何值時,PQ∥BC;
(2)設△AQP的面積為y(cm2),求y關于t的函數關系式,并求出y的最大值;
(3)如圖2,連接PC,并把△PQC沿QC翻折,得到四邊形PQPC,是否存在某時刻t,使四邊形PQP'C為菱形?若存在,求出此時t的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線![]() 與
與![]() 軸,
軸,![]() 軸分別交于點
軸分別交于點![]() ,
,![]() ,與直線
,與直線![]() 交于點
交于點![]() .點
.點![]() 從點
從點![]() 出發以每秒1個單位的速度向點
出發以每秒1個單位的速度向點![]() 運動,運動時間設為
運動,運動時間設為![]() 秒.
秒.
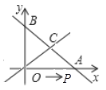
(1)求點![]() 的坐標;
的坐標;
(2)求下列情形![]() 的值;
的值;
①連結![]() ,
,![]() 把
把![]() 的面積平分;
的面積平分;
②連結![]() ,若
,若![]() 為直角三角形.
為直角三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某服裝店用4500元購進一批襯衫,很快售完,服裝店老板又用2100元購進第二批該款式的襯衫,進貨量是第一次的一半,但進價每件比第一批降低了10元.
(1)這兩次各購進這種襯衫多少件?
(2)若第一批襯衫的售價是200元/件,老板想讓這兩批襯衫售完后的總利潤不低于1950元,則第二批襯衫每件至少要售多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com