【題目】如圖是東方貨站傳送貨物的平面示意圖，為了提高安全性，工人師傅打算減小傳送帶與地面的夾角，由原來的45°改為36°，已知原傳送帶BC長為4米，求新傳送帶AC的長及新、原傳送帶觸地點之間AB的長．（結果精確到0.1米）參考數據：sin36°≈0.59，cos36°≈0.1，tan36°≈0.73，
取1.414
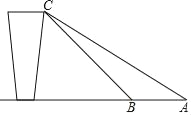
【答案】新傳送帶AC的長為4.8m，新、原傳送帶觸地點之間AB的長約為1.0m．
【解析】
根據題意得出：∠A=36°，∠CBD=45°，BC=4，即可得出BD的長，再表示出AD的長，進而求出AB的長．
如圖，作CD⊥AB于點D，由題意可得：∠A=36°，∠CBD=45°，BC=4．
在Rt△BCD中，sin∠CBD=
，∴CD=BCsin∠CBD=2
．
∵∠CBD=45°，∴BD=CD=2．
在Rt△ACD中，sinA=
，tanA=
，∴AC=
≈
≈4.8，AD=
=
，∴AB=AD﹣BD=﹣2=
﹣2×1.414≈3.87﹣2.83=1.04≈1.0．
答：新傳送帶AC的長為4.8m，新、原傳送帶觸地點之間AB的長約為1.0m．
能考試全能100分系列答案科目：初中數學 來源： 題型：
【題目】甲、乙、丙三明射擊隊員在某次訓練中的成績如下表：
隊員 | 成績（單位：環） | |||||||||
甲 | 6 | 6 | 7 | 7 | 8 | 9 | 9 | 9 | 9 | 10 |
乙 | 6 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 10 |
丙 | 6 | 6 | 6 | 7 | 7 | 8 | 10 | 10 | 10 | 10 |
針對上述成績，三位教練是這樣評價的：
教練
：三名隊員的水平相當；
教練
：三名隊員每人都有自己的優勢；
教練
：如果從不同的角度分析，教練和說的都有道理.
你同意教練的觀點嗎？通過數據分析，說明你的理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】老師所留的作業中有這樣一個分式的計算題：
，甲、乙兩位同學完成的過程分別如下：
甲同學：
第一步
第二步
第三步
乙同學：
第一步
第二步
第三步
老師發現這兩位同學的解答都有錯誤：
(1)甲同學的解答從第______步開始出現錯誤；乙同學的解答從第_____步開始出現錯誤；
(2)請重新寫出完成此題的正確解答過程.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某公司欲招聘廣告策劃人員一名，對甲、乙、丙三名候選人進行三項素質測試，他們的各項測試成績如下表所示：
測試項目 | 測試成績 | ||
甲 | 乙 | 丙 | |
創新 | 72 | 85 | 67 |
綜合知識 | 50 | 74 | 70 |
語言 | 88 | 45 | 67 |
（1）如果根據三項測試的平均成績確定錄用人選，那么誰將被錄用？
（2）根據實際需要，公司將創新、綜合知識、語言三項測試得分按5：3：2的比例確定各人的測試成績，此時誰將被錄用？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知拋物線y=x2+bx+c（b，c是常數）與x軸相交于A，B兩點（A在B的左側），與y軸交于點C．
（1）當A（﹣1，0），C（0，﹣3）時，求拋物線的解析式和頂點坐標；
（2）P（m，t）為拋物線上的一個動點．
①當點P關于原點的對稱點P′落在直線BC上時，求m的值；
②當點P關于原點的對稱點P′落在第一象限內，P′A2取得最小值時，求m的值及這個最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，點A是x軸外的一點，若平面內的點B滿足：線段AB的長度與點A到x軸的距離相等，則稱點B是點A的“等距點”．
（1）若點A的坐標為（0，2），點
（2，2），
（1，
），
（
，1）中，點A的“等距點”是_______________；
（2）若點M（1，2）和點N（1，8）是點A的兩個“等距點”，求點A的坐標；
（3）記函數
（
）的圖象為
，
的半徑為2，圓心坐標為
.若在上存在點M，上存在點N，滿足點N是點M的“等距點”，直接寫出t的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知
是等腰直角三角形，
，點
是
的中點，延長
至點
，使
，連接
（如圖①）.
（1）求證：
≌
；
（2）已知點
是
的中點，連接
（如圖②）.
①求證: ≌
；
②如圖③，延長
至點
，使
，連接
，求證：
.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀探索題：
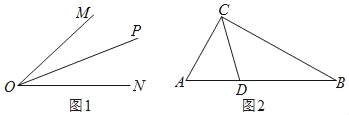
（1）如圖1，OP是∠MON的平分線，以O為圓心任意長為半徑作弧，分別交射線ON、OM于C、B兩點，在射線OP上任取一點A（點O除外），連接AB、AC．求證：△AOB≌△AOC．
（2）請你參考以上方法，解答下列問題：
如圖2，在 Rt△ABC中，∠ACB＝90°，∠A＝60°，CD平分∠ACB，試判斷BC和AC、AD之間的數量關系并證明．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
