
【題目】閱讀理解
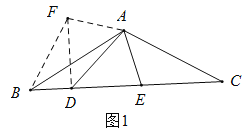
(1)如圖1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 邊上的點,且
邊上的點,且![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的長.
的長.

思考如下:注意到條件中有![]() ,
,![]() ,不妨把
,不妨把![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() ,得到
,得到![]() ,連接
,連接![]() ,易證
,易證![]() ,從而將線段
,從而將線段![]() ,
,![]() ,
,![]() 集中在了
集中在了![]() 中,因為
中,因為![]() 的度數是________;
的度數是________;![]() ,
,![]() 所以
所以![]() 的長為 ;
的長為 ;
類比探究
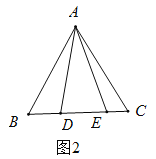
(2)如圖2,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 邊上的點,且
邊上的點,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的長;
的長;
拓展應用
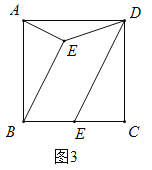
(3)如圖3,![]() 是正方形
是正方形![]() 內一點,
內一點,![]() ,
,![]() 是
是![]() 邊上一點,且
邊上一點,且![]() ,若
,若![]() ,請直接寫出當
,請直接寫出當![]() 取最小值時
取最小值時![]() 的長.
的長.
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根據旋轉的性質可得△ACE≌△ABF,△ADE≌△ADF,得∠ABF=∠ACE=30°, DE=DF,再證明△BDF是直角三角形,運用勾股定理求出DF的長即可得到結論;
(2)將![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() ,得到
,得到![]() ,連接
,連接![]() ,CF, 過點
,CF, 過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() ,方法同(1)證明
,方法同(1)證明![]() 得
得![]() ,求出FG和CG的長,再運用勾股定理即可EF的長,從而得到結論;
,求出FG和CG的長,再運用勾股定理即可EF的長,從而得到結論;
(3)將![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() ,得到
,得到![]() 取
取![]() 的中點
的中點![]() 連接
連接![]() ,
,![]() 取最小值時,點
取最小值時,點![]() 在
在![]() 上,方法同(2)可證明
上,方法同(2)可證明![]() 得OF=OG,在真的三角形BOF中運用勾股定理可求出結論.
得OF=OG,在真的三角形BOF中運用勾股定理可求出結論.
(1)∵AB=AC,∠BAC=120°
∴∠ABC=∠ACB=30°
把![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() ,得到
,得到![]() ,
,
∴△ABF≌△ACE
∴∠ABF=∠ACE=30°
∴∠FBD=60°;
連接![]() ,
,
∵∠BAC=120°,∠DAE=60°,
∴∠BAD+∠CAE=60°
∵∠BAF=∠CAE,
∴∠BAF+∠BAD=60°,即∠DAF=60°
∴∠DAF=∠DAE,
又AF=AE,AD=AD,
∴△DAF≌△DAE,
∴DF=DE
∵BD=1,BF=CE=2,且∠FBD=60°
∴∠BFD=30°,
∴∠BDF=90°,
∴![]()
∴DE=![]()
故答案為:60;![]() ;
;
(2)∵![]() ,
,![]() ,
,
∴![]() 是等邊三角形,
是等邊三角形,
∴![]() ,
,![]()
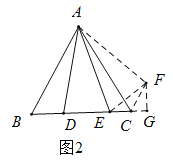
如圖2 ,將![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() ,得到
,得到![]() 連接
連接![]()
則![]() .
.
![]()
![]()
![]()
又![]()
![]()
![]() .
.
如圖2,過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() .
.
![]()
![]()
在![]() 中,
中,![]()
在![]() 中,
中,![]()
![]() .
.
(3)如圖3,將![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() ,得到
,得到![]()
取![]() 的中點
的中點![]() 連接
連接![]() .
.
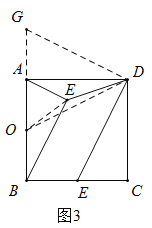
因為![]() ,
,
所以![]() 取最小值時,點
取最小值時,點![]() 在
在![]() 上
上
由![]() 類比,得
類比,得![]() .
.
設![]() 的長為
的長為![]()
則![]() .
.
所以![]() ,
,
解得![]()
∴![]() .
.


 導學全程練創優訓練系列答案
導學全程練創優訓練系列答案科目:初中數學 來源: 題型:
【題目】已知關于 x 的一元二次方程ax2 8x 6 0 .
(1)若方程有實數根,求 a的取值范圍;
(2)若 a為正整數,且方程的兩個根也是整數,求 a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,甲、乙只捕撈船同時從A港出海捕魚,甲船以每小時15![]() km的速度沿北偏西60°方向前進,乙船以每小時15 km的速度沿東北方向前進.甲船航行2 h到達C處,此時甲船發現漁具丟在了乙船上,于是甲船快速(勻速)沿北偏東75°的方向追趕乙船,結果兩船在B處相遇.問:
km的速度沿北偏西60°方向前進,乙船以每小時15 km的速度沿東北方向前進.甲船航行2 h到達C處,此時甲船發現漁具丟在了乙船上,于是甲船快速(勻速)沿北偏東75°的方向追趕乙船,結果兩船在B處相遇.問:
(1)甲船從C處出發追趕上乙船用了多少時間?
(2)甲船追趕乙船的速度是每小時多少千米?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩名隊員參加射擊訓練,成績分別被制成下列兩個統計圖:
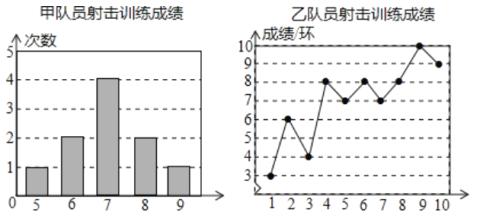
根據以上信息,整理分析數據如下:
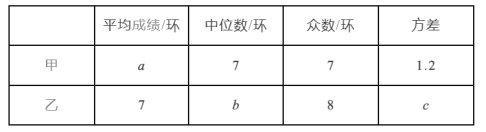
(1)寫出表格中![]() 的值;
的值;
(2)綜合運用上表中的四個統計量,簡要分析這兩名隊員的射擊訓練成績,若選派其中一名參賽,你認為應該選哪名隊員?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,![]() 為坐標原點,點
為坐標原點,點![]() (0,1),點
(0,1),點![]() (1,0),正方形
(1,0),正方形![]() 的兩條對角線的交點為
的兩條對角線的交點為![]() ,延長
,延長![]() 至點
至點![]() ,使
,使![]() .延長
.延長![]() 至點
至點![]() ,使
,使![]() ,以
,以![]() ,
,![]() 為鄰邊做正方形
為鄰邊做正方形![]() .
.
(Ⅰ)如圖①,求![]() 的長及
的長及![]() 的值;
的值;
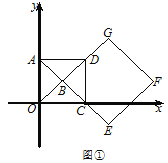
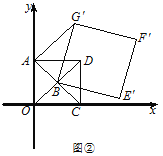
(Ⅱ)如圖②,正方形![]() 固定,將正方形
固定,將正方形![]() 繞點
繞點![]() 逆時針旋轉,得正方形
逆時針旋轉,得正方形![]() ,記旋轉角為
,記旋轉角為![]() (0°<
(0°<![]() <360°),連接
<360°),連接![]() .
.
①旋轉過程中,當![]() 90°時,求
90°時,求![]() 的大小;
的大小;
②在旋轉過程中,求![]() 的長取最大值時,點
的長取最大值時,點![]() 的坐標及此時
的坐標及此時![]() 的大小(直接寫出結果即可).
的大小(直接寫出結果即可).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() 為邊
為邊![]() 上的中線,點
上的中線,點![]() 為
為![]() 延長線上一點,連接
延長線上一點,連接![]() 交
交![]() 于點
于點![]() ,
,![]() ,
,![]() .
.
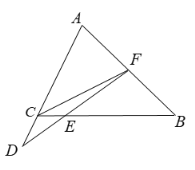
(1)求證:![]() ;
;
(2)在圖中找出與![]() 相等的線段,并證明;
相等的線段,并證明;
(3)若![]() ,求
,求![]() 的值(用含
的值(用含![]() 的代數式表示).
的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知OA是⊙O的半徑,OA=1,點P是OA上一動點,過P作弦BC⊥OA,連接AB、AC.

(1)如圖1,若P為OA中點,則AC=______,∠ACB=_______°;
(2)如圖2,若移動點P,使AB、CO的延長線交于點D.記△AOC的面積為S1,△BOD的面積為S2.△AOD的面積為S3,且滿足![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,P是邊BC上的一動點(不與點B,C重合),點B關于直線AP的對稱點為E,連接AE,連接DE并延長交射線AP于點F,連接BF
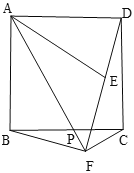
(1)若![]() ,直接寫出
,直接寫出![]() 的大小(用含
的大小(用含![]() 的式子表示).
的式子表示).
(2)求證:![]() .
.
(3)連接CF,用等式表示線段AF,BF,CF之間的數量關系,并證明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com