
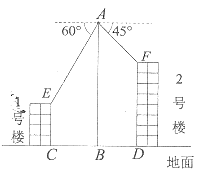
【題目】綜合實踐課上,某興趣小組同學用航拍無人機進行測高實踐,如圖為實踐時繪制的截面圖.無人機從地面點![]() 垂直起飛到達點
垂直起飛到達點![]() 處,測得學校1號樓頂部
處,測得學校1號樓頂部![]() 的俯角為
的俯角為![]() ,測得2號樓頂部
,測得2號樓頂部![]() 的俯角為
的俯角為![]() ,此時航拍無人機的高度為50米.已知1號樓的高度為20米,且
,此時航拍無人機的高度為50米.已知1號樓的高度為20米,且![]() 和
和![]() 分別垂直地面于點
分別垂直地面于點![]() 和
和![]() ,
,![]() 為
為![]() 的中點,求2號樓的高度(結果保留根號).
的中點,求2號樓的高度(結果保留根號).
科目:初中數學 來源: 題型:
【題目】已知:![]() .
.
求作:![]() ,使得
,使得![]() .
.
作法:
①以![]() 為圓心,任意長為半徑畫弧,分別交
為圓心,任意長為半徑畫弧,分別交![]() ,
,![]() 于點
于點![]() ;
;
②畫一條射線![]() ,以點
,以點![]() 為圓心,
為圓心,![]() 長為半徑畫弧,交
長為半徑畫弧,交![]() 于點
于點![]() ;
;
③以點![]() 為圓心,
為圓心,![]() 長為半徑畫弧,與第②步中所畫的弧相交于點
長為半徑畫弧,與第②步中所畫的弧相交于點![]() ;
;
④過點![]() 畫射線
畫射線![]() ,則
,則![]() .
.
根據上面的作法,完成以下問題:
(1)使用直尺和圓規,作出![]() (請保留作圖痕跡).
(請保留作圖痕跡).
(2)完成下面證明![]() 的過程(注:括號里填寫推理的依據).
的過程(注:括號里填寫推理的依據).
證明:由作法可知![]() ,
,![]() ,
,![]() ,
,
∴![]() ≌
≌![]() ( )
( )
∴![]() .( )
.( )
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某海監船以60海里/時的速度從A處出發沿正西方向巡邏,一可疑船只在A的西北方向的C處,海監船航行1.5小時到達B處時接到報警,需巡査此可疑船只,此時可疑船只仍在B的北偏西![]() 方向的C處,然后,可疑船只以一定速度向正西方向逃離,海監船立刻加速以90海里/時的速度追擊,在D處海監船追到可疑船只,D在B的北偏西
方向的C處,然后,可疑船只以一定速度向正西方向逃離,海監船立刻加速以90海里/時的速度追擊,在D處海監船追到可疑船只,D在B的北偏西![]() 方同.(以下結果保留根號)
方同.(以下結果保留根號)
(1)求B,C兩處之問的距離;
(2)求海監船追到可疑船只所用的時間.

查看答案和解析>>
科目:初中數學 來源: 題型:
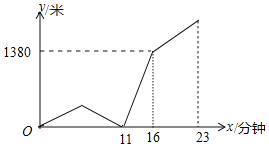
【題目】一天,小明從家出發勻速步行去學校上學.幾分鐘后,在家休假的爸爸發現小明忘帶數學書,于是爸爸立即勻速跑步去追小明,爸爸追上小明后以原速原路跑回家.小明拿到書后以原速的![]() 快步趕往學校,并在從家出發后23分鐘到校(小明被爸爸追上時交流時間忽略不計).兩人之間相距的路程y(米)與小明從家出發到學校的步行時間x(分鐘)之間的函數關系如圖所示,則小明家到學校的路程為________米.
快步趕往學校,并在從家出發后23分鐘到校(小明被爸爸追上時交流時間忽略不計).兩人之間相距的路程y(米)與小明從家出發到學校的步行時間x(分鐘)之間的函數關系如圖所示,則小明家到學校的路程為________米.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線y=ax2+bx+c(a<0)經過點(-1,0),且滿足4a+2b+c>0.以下結論(1)a+b>0;(2)a+c>0;(3)-a+b+c>0;(4)b2-2ac>5a2其中正確的個數有( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
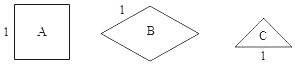
【題目】將圖中的![]() 型(正方形)、
型(正方形)、![]() 型(菱形)、
型(菱形)、![]() 型(等腰直角三角形)紙片分別放在
型(等腰直角三角形)紙片分別放在![]() 個盒子中,盒子的形狀、大小、質地都相同,再將這
個盒子中,盒子的形狀、大小、質地都相同,再將這![]() 個盒子裝入一只不透明的袋子中.
個盒子裝入一只不透明的袋子中.
(1)攪勻后從中摸出![]() 個盒子,盒中的紙片既是軸對稱圖形又是中心對稱圖形的概率是 ;
個盒子,盒中的紙片既是軸對稱圖形又是中心對稱圖形的概率是 ;
(2)攪勻后先從中摸出![]() 個盒子(不放回),再從余下的
個盒子(不放回),再從余下的![]() 個盒子中摸出
個盒子中摸出![]() 個盒子,把摸出的
個盒子,把摸出的![]() 個盒中的紙片長度相等的邊拼在一起,求拼成的圖形是軸對稱圖形的概率.(不重疊無縫隙拼接)
個盒中的紙片長度相等的邊拼在一起,求拼成的圖形是軸對稱圖形的概率.(不重疊無縫隙拼接)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數:![]() .
.
(1)求證:二次函數的圖象與x軸有兩個交點;
(2)當二次函數的圖象與x軸的兩個交點的橫坐標均為整數,且a為負整數時,求a的值及二次函數的解析式并畫出二次函數的圖象(不用列表,只要求用其與x軸的兩個交點A,B(A在B的左側),與y軸的交點C及其頂點D這四點畫出二次函數的大致圖象,同時標出A,B,C,D的位置);
(3)在(2)的條件下,二次函數的圖象上是否存在一點P使![]() ?如果存在,求出點P的坐標;如果不存在,請說明理由.
?如果存在,求出點P的坐標;如果不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點D在⊙O的直徑AB延長線上,點C在⊙O上,過點D作ED⊥AD,與AC的延長線相交于點E,且CD=DE.
(1)求證:CD為⊙O的切線;
(2)若AB=12,且BC=CE時,求BD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某大樓的頂部樹有一塊廣告牌CD,小李在山坡的坡腳A處測得廣告牌底部D的仰角為60°.沿坡面AB向上走到B處測得廣告牌頂部C的仰角為45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的鉛直高度BH與水平寬度AH的比)
是指坡面的鉛直高度BH與水平寬度AH的比)

(1)求點B距水平面AE的高度BH;
(2)求廣告牌CD的高度.
(測角器的高度忽略不計,結果精確到0.1米.參考數據:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com