
【題目】拋物線![]() 與
與![]() 軸相交于
軸相交于![]() 兩點(diǎn),與
兩點(diǎn),與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() .
.
(1)設(shè)![]() ,求該拋物線的解析式;
,求該拋物線的解析式;
(2)在⑴中,若點(diǎn)![]() 為直線
為直線![]() 下方拋物線上一動(dòng)點(diǎn),當(dāng)⊿
下方拋物線上一動(dòng)點(diǎn),當(dāng)⊿![]() 的面積最大時(shí),求點(diǎn)
的面積最大時(shí),求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(3)是否存在整數(shù)![]() 使得
使得![]() 和
和![]() 同時(shí)成立,請(qǐng)證明你的結(jié)論.
同時(shí)成立,請(qǐng)證明你的結(jié)論.
【答案】(1)拋物線解析式為![]() ;
;
(2)![]() ;
;
(3)不存在整數(shù)![]() 使得
使得![]() 和
和![]() 同時(shí)成立,證明見解析.
同時(shí)成立,證明見解析.
【解析】試題分析:本題的⑴問中由于拋物線上沒有現(xiàn)成的坐標(biāo),所以要根據(jù)一元二次方程根與系數(shù)的關(guān)系,并結(jié)合三角函數(shù)和二次函數(shù)的對(duì)稱軸進(jìn)行多次代數(shù)轉(zhuǎn)換即可求出二次函數(shù)的待定系數(shù)![]() ,其轉(zhuǎn)換有點(diǎn)繁瑣,可以分步進(jìn)行.
,其轉(zhuǎn)換有點(diǎn)繁瑣,可以分步進(jìn)行.
關(guān)于面積的“最值”問題一般都要通過建立二次函數(shù)切入來解決問題,本題的⑵問可采用“割補(bǔ)法”來表示⊿![]() 的面積.若采取“補(bǔ)”的辦法,可以連接
的面積.若采取“補(bǔ)”的辦法,可以連接![]() ,此時(shí)⊿
,此時(shí)⊿![]() 的面積可以看作是四邊形
的面積可以看作是四邊形![]() 的面積減去⊿
的面積減去⊿![]() 的面積,即
的面積,即![]() ⊿
⊿![]() =
= ![]() ⊿
⊿![]() + (或 -)
+ (或 -)![]() ⊿
⊿![]() -
- ![]() ⊿
⊿![]() ,由于在⑴問中我們能把原二次函數(shù)的解析式求出來,在此基礎(chǔ)上求出
,由于在⑴問中我們能把原二次函數(shù)的解析式求出來,在此基礎(chǔ)上求出![]() 的坐標(biāo),然后把
的坐標(biāo),然后把![]() 的橫縱坐標(biāo)均用自變量表示出來,在此基礎(chǔ)上建立關(guān)于⊿
的橫縱坐標(biāo)均用自變量表示出來,在此基礎(chǔ)上建立關(guān)于⊿![]() 的面積的二次函數(shù)使問題可以解決.(本問也可以采用過點(diǎn)
的面積的二次函數(shù)使問題可以解決.(本問也可以采用過點(diǎn)![]() 作
作![]() 軸的垂線把⊿
軸的垂線把⊿![]() “割”成兩個(gè)三角形來解答,計(jì)算量相當(dāng).)
“割”成兩個(gè)三角形來解答,計(jì)算量相當(dāng).)
本題的⑶問是一個(gè)存在性的問題.先假設(shè)存在,然后結(jié)合![]() 和
和![]() 利用根與系數(shù)的關(guān)系解出
利用根與系數(shù)的關(guān)系解出![]() 的分別的整數(shù)值,在此基礎(chǔ)上分析圖象信息所得出的條件,分別代入討論,即可使問題獲得解決.
的分別的整數(shù)值,在此基礎(chǔ)上分析圖象信息所得出的條件,分別代入討論,即可使問題獲得解決.
試題解析:(1)根據(jù)題中的![]()
可知: 
∴![]() ,
,
配方得: ![]() .分別代入得:
.分別代入得: ![]() ①
①
∵![]()
∴![]() ;
;
又拋物線與![]() 軸的交點(diǎn)為
軸的交點(diǎn)為![]() ,
,
∴![]()
∵拋物線對(duì)稱軸為![]() ,
,
即![]() ,
,
又![]() ,
,
∴![]() .
.
∴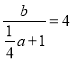 ②,
②,
把①②聯(lián)立后解得: ![]() 或
或![]() (舍去).
(舍去).
把![]() 代入①得:
代入①得: ![]() .
.
∴拋物線解析式為![]() .
.
⑵.連結(jié)![]() ,過點(diǎn)
,過點(diǎn)![]() 分別向坐標(biāo)作高
分別向坐標(biāo)作高![]() (見后面的圖示)
(見后面的圖示)

若設(shè)點(diǎn)![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() ,代入
,代入![]() 后得到
后得到![]() ,
,
即點(diǎn)![]() 的橫縱坐標(biāo)為
的橫縱坐標(biāo)為![]() .
.
則![]() .
.
在![]() 中,令
中,令![]() 時(shí),
時(shí), ![]() ;
;
即與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
令![]() 時(shí),解得:
時(shí),解得: ![]()
即與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
∴![]() ⊿
⊿![]() =
= ![]() ⊿
⊿![]() +
+ ![]() ⊿
⊿![]() -
- ![]() ⊿
⊿![]() =
= ![]()
①當(dāng)![]() 時(shí),
時(shí), ![]() .
.
∵二次項(xiàng)系數(shù)![]()
∴![]() 沒有最大值.
沒有最大值.
②當(dāng)![]() 時(shí),
時(shí), ![]() .
.
∵二次項(xiàng)系數(shù)![]()
∴![]() 有最大值.當(dāng)
有最大值.當(dāng)![]() 時(shí),
時(shí), ![]() 有最大值
有最大值![]() .
.
∴![]() .
.
⑶假設(shè)存在整數(shù)![]() ,并且使得
,并且使得![]() 和
和![]() 同時(shí)成立.、
同時(shí)成立.、
根據(jù)題意有: ![]() 即
即
解得: ![]()
∵![]() 為整數(shù)
為整數(shù)
∴![]()
對(duì)于拋物線![]() 與
與![]() 軸相交于
軸相交于![]() 兩點(diǎn).
兩點(diǎn).
若要同時(shí)存在![]() 和
和![]() 說明:
說明:
①此時(shí)的拋物線開口向上且與![]() 軸在
軸在![]() 兩個(gè)點(diǎn)之間(不含這兩個(gè)點(diǎn))有兩個(gè)交點(diǎn).;
兩個(gè)點(diǎn)之間(不含這兩個(gè)點(diǎn))有兩個(gè)交點(diǎn).;
②當(dāng)![]() 時(shí),
時(shí), ![]() ;
;
③當(dāng)![]() 時(shí),
時(shí), ![]() .
.
∴ ①![]() ;②
;②![]() ;③
;③![]() ; 又④
; 又④![]() 要為整數(shù).
要為整數(shù).
∴把![]() 代入①②③④解得
代入①②③④解得![]() 無解;
無解;
把![]() 代入①②③④解得
代入①②③④解得![]() 無解;
無解;
把![]() 代入①②③④解得
代入①②③④解得![]() 無解.
無解.
綜上所述不存在整數(shù)![]() 使得
使得![]() 和
和![]() 同時(shí)成立.
同時(shí)成立.


 名校通行證有效作業(yè)系列答案
名校通行證有效作業(yè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知直線l1:y1=x+m與直線l2:y2=nx+3相交于點(diǎn)A(1,2).
(1)求m、n的值;
(2)設(shè)l1交x軸于點(diǎn)B,l2交x軸于點(diǎn)C,若點(diǎn)D與點(diǎn)A,B,C能構(gòu)成平行四邊形,請(qǐng)直接寫出D點(diǎn)坐標(biāo);
(3)請(qǐng)?jiān)谒o坐標(biāo)系中畫出直線l1和l2 , 并根據(jù)圖象回答問題:
當(dāng)x滿足時(shí),y1>2;
當(dāng)x滿足時(shí),0<y2≤3;
當(dāng)x滿足時(shí),y1<y2 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】木工師得要將一根木條固定在墻上,通常需要釘兩根釘子,請(qǐng)你寫出這一現(xiàn)象反映的一個(gè)數(shù)學(xué)基本事實(shí)______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如果一個(gè)正比例函數(shù)的圖象經(jīng)過不同象限的兩點(diǎn)A(2,m),B(n,3),那么一定有( )
A.m>0,n>0
B.m>0,n<0
C.m<0,n>0
D.m<0,n<0
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() 、
、![]() 兩點(diǎn)在
兩點(diǎn)在![]() 上,
上,![]() 、
、![]() 兩邊分別與
兩邊分別與![]() 邊交于點(diǎn)
邊交于點(diǎn)![]() 、
、![]() .固定
.固定![]() 不動(dòng),
不動(dòng),![]() 從點(diǎn)
從點(diǎn)![]() 與點(diǎn)
與點(diǎn)
B重合的位置出發(fā),沿![]() 邊以每秒
邊以每秒![]() 個(gè)單位的速度向點(diǎn)
個(gè)單位的速度向點(diǎn)![]() 運(yùn)動(dòng);同時(shí)點(diǎn)
運(yùn)動(dòng);同時(shí)點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā),在折線
出發(fā),在折線![]() 上
上
以每秒![]() 個(gè)單位的速度向點(diǎn)
個(gè)單位的速度向點(diǎn)![]() 運(yùn)動(dòng).當(dāng)點(diǎn)
運(yùn)動(dòng).當(dāng)點(diǎn)![]() 到達(dá)點(diǎn)
到達(dá)點(diǎn)![]() 時(shí),
時(shí),![]() 和點(diǎn)
和點(diǎn)![]() 同時(shí)停止運(yùn)動(dòng).設(shè)運(yùn)動(dòng)時(shí)間為
同時(shí)停止運(yùn)動(dòng).設(shè)運(yùn)動(dòng)時(shí)間為![]() (秒).
(秒).

(1)當(dāng)![]() 時(shí),
時(shí),![]() __________
__________![]() ,
,![]() __________
__________![]() .
.
(2)當(dāng)![]() 為何值時(shí),
為何值時(shí),![]() 為等腰三角形?請(qǐng)說明理由.
為等腰三角形?請(qǐng)說明理由.
(3)當(dāng)![]() 為何值時(shí),點(diǎn)
為何值時(shí),點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 重合?寫出計(jì)算過程.
重合?寫出計(jì)算過程.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】若一元二次方程x2﹣4x+3=0的兩個(gè)實(shí)數(shù)根分別是a、b,則一次函數(shù)y=abx+a+b的圖象一定不經(jīng)過( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】若等腰三角形的兩邊長(zhǎng)分別是6cm和4cm,則等腰三角形的周長(zhǎng)是( )
A. 16cm B. 14cm C. 16cm或14cm D. 無法確定
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com